八皇后和八数码问题

Posted on |

Generate a large number of 8-puzzle and 8-queens instances and solve them(where possible) by hill climbing (steepest-ascent and first-choice variants), hill climbing with random restart, and simulated annealing. Measure the search cost and percentage of solved problems and graph these against the optimal solution cost. Comment on your results.

问题描述

生成大量的八数码问题和八皇后问题并用以下算法分别求解：爬山法（最陡上升和首选爬山法），随机重启爬山法，模拟退火算法。计算搜索耗散和问题的解决率，并用图对比它们的最优解代价的曲线。对结果进行评估。

Github完整代码及测试结果

参考资料
《人工智能：一种现代的方法》
N-Queens
爬山法、随机重启爬山法、模拟退火算法对八皇后问题和八数码问题的性能测试

八皇后问题

符号说明及实例生成和调用

上图的表示方法为：board[5,0,4,2,8,2,7,3]

随机生成一千个实例写入文件

testCaseGenerator.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import random
def main():
    f = open("eightQueensTest.txt", "wb")
    testCaseCount = 1000
    board = ""
    while testCaseCount > 0:
        testCaseCount -= 1
        for col in range(0,7):
            board += str(random.randint(0,7)) + ' '
        board += str(random.randint(0,7)) + '\n'
    f.write(board)
    f.close()
    
if __name__ == '__main__':
    main()

在每种方法的主函数中读文件获得实例并调用方法求解问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
with open("eightQueensTest.txt", "r") as ins:
    for line in ins:
        print "case: ", totalCase
        global FAILED
        FAILED = False
        totalCase += 1
        board = []
        for col in line.split():
            board.append(int(col))
        board = solution_FirstChoiceHillClimbing(board) # 换成对应的方法
        if FAILED:
            result += "Failed!"
        else:
            successCase += 1
            for col in range(len(board)):
                result += str(board[col]) + " "
        result += "\n"

启发式代价

用互相攻击的皇后数表示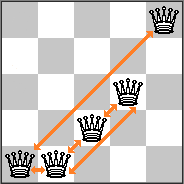

1
2
3
4
5
6
7
8
9
10
# heuristic cost
def getCollisionNum(board):
    num = 0
    for col in range(len(board)):
        for anotherCol in range(col+1, len(board)):
            if board[col] == board[anotherCol]:
                num += 1 # collied in the same row
            elif abs(board[col] - board[anotherCol]) == (anotherCol - col):
                num += 1 # collied diagonally
    return num

四种方法的单步操作

最陡上升爬山法

计算当前棋盘所有空位置（该列的皇后挪动到该行）的启发式代价（互相攻击皇后数），选择代价最低的。

例如下图中将第二列的皇后放置到第二行冲突数最小，为2。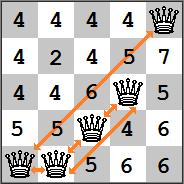

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# for each column, calculate the collision number
# if the queen is moved to the other rows
# find the smallest one and move to it.
def step_steepestHillClimbing(board):
    collisionNumBoard = {}
    smallestCollisionNum = getCollisionNum(board)
    for col in range(len(board)):
        for row in range(len(board)):
            if board[col] == row:
                continue
            originRow = board[col]
            board[col] = row
            collisionNumBoard[(row,col)] = getCollisionNum(board)
            board[col] = originRow
    
    
    for point,value in collisionNumBoard.iteritems():
        if value < smallestCollisionNum:
            smallestCollisionNum = value
    
    smallestCollisionPoints = []
    for point,value in collisionNumBoard.iteritems():
        if value == smallestCollisionNum:
            smallestCollisionPoints.append(point)
    
    # can not find a steeper move
    # we have come to the peek(local optimization)
    if len(smallestCollisionPoints) == 0:
        #print "local optimization"
        global FAILED
        FAILED = True
        return board
    
    random.shuffle(smallestCollisionPoints)
    board[smallestCollisionPoints[0][1]]=smallestCollisionPoints[0][0]
    return board

首选爬山法

随机选择一个空位置，若该位置优于当前棋盘，则选择之。
注意，此处“优于”指“冲突数小于等于”，因为经测试，接受冲突数和当前棋盘一样的情况，可大大提高求解率。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# randomly select a point until it is 
# better than the original one
# change "better than" to "not worse than"
# can significantly increase the success rate
def step_FirstChoiceHillClimbing(board):
    collisionNum = getCollisionNum(board)
    maxRound = 1000
    count = 0
    while True:
        count += 1
        if(count >= maxRound):
            global FAILED
            FAILED = True
            return board
        randomRow = random.randint(0,len(board)-1)
        randomCol = random.randint(0,len(board)-1)
        if board[randomCol] == randomRow:
            continue
        originRow = board[randomCol]
        board[randomCol] = randomRow
        if getCollisionNum(board) <= collisionNum: # not worse than
            return board
        board[randomCol] = originRow

随机重启爬山法

随机选择一个空位置。

1
2
3
4
5
6
7
8
9
def step_RandomHillClimbing(board):
    while True:
        randomRow = random.randint(0,len(board)-1)
        randomCol = random.randint(0,len(board)-1)
        if board[randomCol] != randomRow:
            board[randomCol] = randomRow
            return board
    
    return board

模拟退火算法

结合了爬山法，随机选一个空位置，若冲突数更小，则移动到那里。反之，以一定概率接受更差的选择，避免高不成低不就。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# accept the random choice with certain probability
def step_SimulatedAnnealing(board):
    temperature = len(board)**2
    annealingRate = 0.95
    while True:
        randomRow = random.randint(0,len(board)-1)
        randomCol = random.randint(0,len(board)-1)
        originCollisionNum = getCollisionNum(board)
        originRow = board[randomCol]
        board[randomCol] = randomRow
        newCollisionNum = getCollisionNum(board)
        temperature = max(temperature * annealingRate, 0.02)
        if newCollisionNum < originCollisionNum:
            return board
        else:
            deltaE = newCollisionNum - originCollisionNum
            acceptProbability = min(math.exp(deltaE / temperature), 1)
            if random.random() <= acceptProbability:
                return board
            else:
                board[randomCol] = originRow
    
    return board

结果对比

每种方法写solution函数一定次数内循环调用step函数, 例如

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def solution_FirstChoiceHillClimbing(board):
    maxRound = 200 # the expected number to find a solution
    count = 0
    while True:
        collisionNum = getCollisionNum(board)
        if collisionNum == 0:
            return board
        board = step_FirstChoiceHillClimbing(board)
        global FAILED
        if FAILED:
            return board
        count += 1
        if(count >= maxRound):
            FAILED = True
            return board

注意，每种方法的预期能找到解或失败的循环次数和方法相关。例如最陡上升爬山法有找到解和达到局部最优解或平原地带而陷入循环两种状态。通过测试，200步是合理的预期步数。而模拟退火算法经测试通常在万步级（几万/几十万步）找到解，具体来说是500000步内，不排除超出的情况，处于时间考虑，将超出50万步的视为失败。

对一千个随机生成的样例进行测试并对比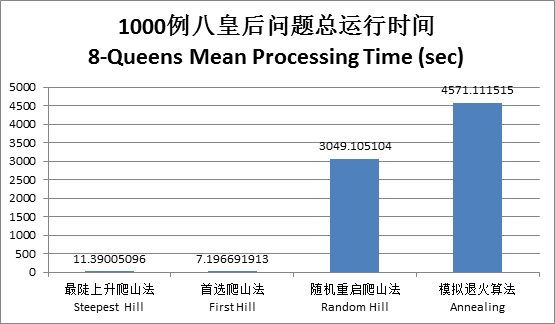

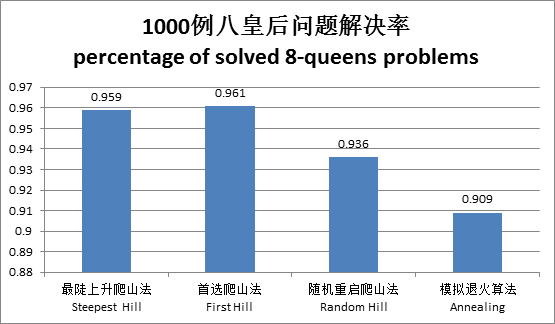
数据显示，四种方法对于八皇后问题的解决率都在90%以上，差距不明显。首选爬山法相对较优，模拟退火算法相对较劣。而时间上差距悬殊，最陡上升爬山法和首选爬山法用时极少，随机重启爬山法和模拟退火算法用时极多。相对快的首选爬山法比相对慢的模拟退火算法快了约六百倍。综合来看，首选爬山法最优，最陡上升爬山法稍次之，另两种方法在时间上可以淘汰了。

八数码问题

符号说明及实例生成和调用

上图是目标状态，0表示空白方块，其他数字可以移动到该位置。代码中用board[0,1,2,3,4,5,6,7,8]来表示

随机生成一千个实例写入文件

从目标状态开始，随机移动空白块一定次数（如5000次）生成实例来确保有解

testCaseGenerator.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
import random
def step_RandomHillClimbing(board):
    for i in range(len(board)):
        if board[i] == 0:
            break
    while True:
        randCase = random.randint(0,4)
        if randCase == 0:
            if i >= 3:
                upBoard = list(board)
                upBoard[i] = board[i-3]
                upBoard[i-3] = 0
                return upBoard
        elif randCase == 1:
            if i < 6:
                downBoard = list(board)
                downBoard[i] = board[i+3]
                downBoard[i+3] = 0
                return downBoard
        elif randCase == 2:
            if i%3 != 0:
                leftBoard = list(board)
                leftBoard[i] = board[i-1]
                leftBoard[i-1] = 0
                return leftBoard
        else:    
            if (i+1)%3 != 0:
                rightBoard = list(board)
                rightBoard[i] = board[i+1]
                rightBoard[i+1] = 0
                return rightBoard
        
    return board
def solution_RandomHillClimbing(board):
    maxStep = 5000
    count = 0
    while True:
        board = step_RandomHillClimbing(board)
        count += 1
        if(count >= maxStep):
            return board
    
def main():
    f = open("eightPuzzleTest.txt", "wb")
    testCaseCount = 1000
    result = ""
    while testCaseCount > 0:
        board = [0,1,2,3,4,5,6,7,8]
        testCaseCount -= 1
        
        board = solution_RandomHillClimbing(board)
        
        for i in range(0,8): # i = 0 1 2 3 4 5 6 7
            result += str(board[i]) + ' '
        result += str(board[i+1]) + '\n' #! i+1=8
    print result
    f.write(result)
    f.close()
    
if __name__ == '__main__':
    main()

在每种方法的主函数中读文件获得实例并调用方法求解问题（和八皇后问题类似，不再赘述）

启发式代价

每个数码到目标位置的曼哈顿距离之和，为0时找到解

1
2
3
4
5
6
7
# heuristic cost
# manhattan_distance
def getManhattanDistance(board):
    distance = 0
    for i in range(len(board)):
        distance += abs(i/3 - board[i]/3) + abs(i%3 - board[i]%3)
    return distance

四种方法的单步操作

方法同八皇后，欲知详情，点我。

结果对比

同八皇后问题，每种方法写solution函数一定次数内循环调用step函数

对一千个随机生成的样例进行测试并对比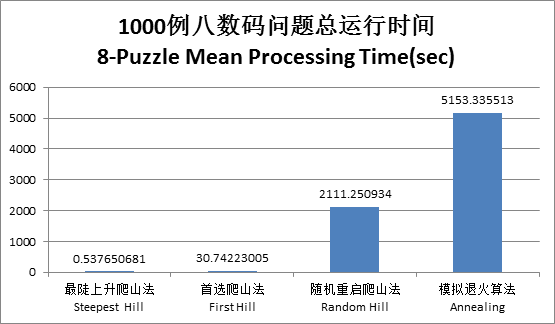

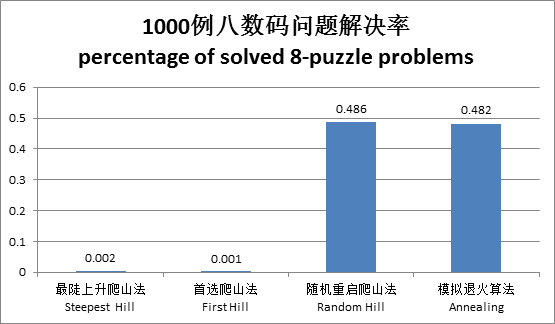
从跑的结果来看，时间上和八皇后问题态势接近，解决率却大相径庭。随机重启爬山法和模拟退火算法的解决率不到百分之五十，原来高高在上的最陡上升爬山法和首选爬山法这次的解决率不忍直视。

这是为什么呢？

八皇后问题一个棋盘有8*8-8=56个随机选择，八皇后问题在不考虑旋转与翻转等价时,共有92 个不同的解，考虑时解更多，因此比当前棋盘更优的选择不会少。每次都能减少一点冲突，很快就太平了。

八数码问题一个棋盘的随机选择数在2到4之间，比当前棋盘更优的选择寥寥。经试验，大量棋盘会卡在局部最优解（局部顶峰/平原）而被判失败。意思是空白块左看右看上看下看都没有更好的选择了，但就是不走更差的那条路，那就…堵着吧。

总的来说，最陡上升爬山法傲娇，首选爬山法贪婪，随机重启爬山法盲目，模拟退火算法谨慎又大胆。（以上词不分褒贬）

以上写得非常简略，感觉有一千句话只写了一句，见谅T T。博主要受使命召唤去打怪了！