详细探讨解决Kaggle上某回归/分类比赛的全过程。包括用线性回归之梯度下降法/正规方程法（MATLAB）、神经网络之多层感知器（TensorFlow）、最近邻（scikit-learn）进行回归预测和用逻辑回归之梯度上升法（Python）、梯度提升决策树（XGBoost）进行分类预测。读者将理解线性回归和逻辑回归的原理/实现、其他框架的使用/调参，以及如何利用Python的多进程对逻辑回归的运算进行并行化提高效率。

目录(Table of Contents)

请点击页面右下角的小图标查看详细目录

目录(Table of Contents)
回归(Regression)
2.1. 数据(Data)
2.2. 度量标准(Evaluation)
2.3. 线性回归(linear regression)
2.3.1. 线性模型(linear model)
2.3.2. 线性回归(linear regression)
2.3.3. 梯度下降法(Gradient Descent)
2.3.4. 正规方程(Normal Equation)
2.4. 多层感知器(Multi-layer Perceptron, MLP)
2.5. 最近邻之scikit-learn
2.6. 各回归方法对比
分类(Classification)
3.1. 数据(Data)
3.2. 度量标准(Evaluation)
3.3. 逻辑回归(Logistic Regression)
3.3.1. Hypothesis Representation
3.3.2. 梯度上升法
3.3.3. 梯度下降法
3.3.4. 梯度法分类及实现
3.3.5. 并行化
3.3.6. 结果及比较
3.4. GBDT之XGBoost
Reference & Futher Reading

回归(Regression)

Predicting a continuous-valued attribute (continuous labels) associated with an object.

回归预测的是连续的值。
Kaggle link: Linear Regression-SYSU-2017

数据(Data)

save_train.csv
The format of each line is id,value0,value1,...,value383,reference where value0,value1,…,value383 are the features.
save_test.csv
This file contains the features whose references you need to predict. The format of each line is id,value0,value1,...,value383.
sample_submission.csv (or result.csv)
The format of each line is id,reference.

度量标准(Evaluation)

RMSE (Root Mean Squared Error)
越小越好

线性回归(linear regression)

线性模型(linear model)

给定由n个属性描述的示例$\mathbf{x}=(x_1;x_2;…;x_n)$，其中$x_i$是$\mathbf{x}$在第$i$个属性上的取值，线性模型试图学得一个通过属性的线性组合来进行预测的函数，即
$$h_{\mathbf{\theta}}(\mathbf{x})={\Theta}^T\mathbf{x}={\theta}_1x_1+{\theta}_2x_2+…+{\theta}_nx_n+b$$
$b$是常数项，通过引入$x_0=1$（截距intercept term），即令${\theta}_0x_0=b$，可以简化表达式。
$$h_{\mathbf{\theta}}(\mathbf{x})=\displaystyle \sum_{ i = 0 }^{ n } {\theta}_ix_i={\Theta}^T\mathbf{x}$$
$\Theta$和$b$学得之后，模型就得以确定。
线姓模型形式简单、易于建模，许多更为强大的非线性模型(nonlinear model)可在线性模型的基础上通过引入层次结构或高维映射得到。此外，由于$\Theta$直观地表达了各属性在预测中的重要性，线性模型有很好的可解释性(comprehensibility)。

线性回归(linear regression)

给定数据集$D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_m,y_m)\}$，其中$\mathbf{x}_i=(x_{i1};x_{i2};…;x_{in}),y_i \in \mathbb{ R }$.“线性回归”试图学得一个线性模型以尽可能准确地预测实值输出标记。即学得

$$h_{\mathbf{\theta}}(\mathbf{x})={\Theta}^T\mathbf{x},使得h_{\mathbf{\theta}}(x_i) \simeq y_i$$

为了刻画$h_{\mathbf{\theta}}(x_i)$和$y_i$之间的差距，定义代价函数(cost function)：

$$J(\theta)=\frac{1}{2}\displaystyle \sum_{ i = 1 }^{ m } (h_\theta(x^{(i)})-y^{(i)})^2$$

目标是找到使代价函数尽量小的$\theta$。具体的学习方法，可参考《机器学习》第3章

接下来将讨论两种解线性回归的方法：梯度下降法和正规方程法。

梯度下降法(Gradient Descent)

推荐阅读：CS229 Lecture notes1 Part I

算法概观

式子$h_{\theta}(x)={\theta}^Tx={\theta}_0x_0+{\theta}_1x_1+{\theta}_2x_2+…+{\theta}_nx_n$中的$x_1…x_n$是特征/变量，${\theta}_1…{\theta}_n$是待求参数。

梯度下降法是解决线性回归的一种方法。思路是选择一个初始的$\theta$值，并重复进行更新$\theta$以使得代价函数$J(\theta)$一直减小，直到达到极小值。具体算法是重复下面的步骤（同步更新$j=0,…,n$）：
$$\theta_j:=\theta_j-\alpha\frac{ \partial }{ \partial \theta_j }J(\theta)$$

梯度“下降”的含义

更新规则（上式）中的减号用于最小化代价函数，这就是下降最直接的含义。
$\alpha$是学习率(learning rate)，梯度下降算法每次在$J$下降最快的方向走了一步，表现为找到的参数对应的代价“下降”。简化、直观的理解见下图：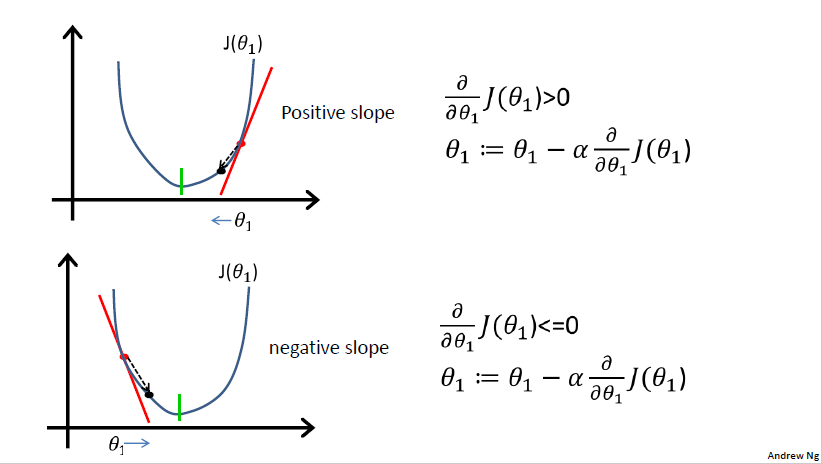

图中的$\frac{ \partial }{ \partial \theta_j }J(\theta)$是偏导数(partial derivative)，Positive slope表示切线斜率(slope of the tangent)为正（反之为负），它们和梯度(gradient)的关系是

If f(x1, …, xn) is a differentiable, real-valued function of several variables, its gradient is the vector whose components are the n partial derivatives of f. Like the derivative, the gradient represents the slope of the tangent of the graph of the function. (wiki)

值得注意的是，在梯度下降法的迭代过程中梯度也在下降：梯度是有方向的向量，由多个偏导数组成。梯度代表了切线斜率。从图二可以看出，无论梯度（切线斜率）初始为正还是负，在迭代过程中都会减小，减小到0时意味着找到了极小值，终止迭代。
但不能认为梯度上升法中的梯度在上升（读者可以一个向上凸的代价函数为例思考），“上升”可理解为加号用于最大化函数（在后文将讨论的逻辑回归法中指参数概率$L(\theta)$而不是代价函数，代价函数总是应该被最小化）。

梯度“下降”证明

梯度下降方法在选取的$\alpha$足够小、迭代运算次数足够多的情况下可以确保每次迭代$J$都减小并达到极小值。证明如下：
设代价函数上某点$\theta_1$，在$\alpha$足够小的正数时，迭代一步更新为$\theta_1^*=\theta_1-\alpha\frac{ \partial }{ \partial \theta_1}J(\theta_1)$.可认为$\theta_1$与$\theta_1^*$之间的曲线和曲线上点$\theta_1$处的切线重合，切线斜率$k$等于偏导数：
$$k=\frac{ \partial }{ \partial \theta_1 }J(\theta_1=\theta_1^*)$$ 又代价函数在$\theta_1$的值用点斜式可以表示为
$$J(\theta_1)=k\theta_1+b$$ 在$\theta_1^*$的值表示为
$$J(\theta_1^*)=k\theta_1^*+b=k(\theta_1-\alpha\frac{ \partial }{ \partial \theta_1}J(\theta_1))+b$$ 结合上面三个式子计算得到
$$J(\theta_1^*)-J(\theta_1)=\alpha(\frac{ \partial }{ \partial \theta_1}J(\theta_1))^2\geq0$$ 大部分情况下两者之差是正数，说明J在减小。若两者之差为0，即偏导数为0，说明已收敛到极小值处，可以停止计算了。

计算偏导数

图一中的偏导数进一步计算（此处省略计算过程）得到$\frac{ \partial }{ \partial y }J(\theta)=\frac{1}{m}\displaystyle \sum_{ i = 1 }^{ m } (h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$，即下图

用MATLAB实现

读写数据及测试

注：这些是公共模块，后面不再赘述

读数据并给$\mathbf{x}$加上常数项(intercept term)：

%% Load Data
fprintf('Loading data ...\n');
train_data = csvread('../data/save_train.csv', 1, 1);
X_train = train_data(:, 1:384);
y_train = train_data(:, 385);
m = length(y_train);
% Add intercept term to X
X_train = [ones(m, 1) X_train];

使用计算获得的$\theta$参数进行预测并写文件：

%% Test and write to file
fprintf('Testing ...\n');
X_test = csvread('../data/save_test.csv', 1, 1);
X_test = [ones(m, 1) X_test];
predict_data = X_test * theta;
fprintf('Writing to file ...\n');
headers = {'id','reference'};
data = table((0:24999)', predict_data, 'VariableNames', headers);
writetable(data, 'result.csv')

梯度下降实现

在实践中，数据应当进行预处理，将特征缩放(feature scaling)到相似的尺度（如$-1 \leq 1$），本例中的数据符合要求，因此跳过了这个步骤。
初始化。alpha及num_iters的值需根据不同的数据调整。本例中alpha=0.1-0.001可以较理想的速度收敛，num_iters=50000后收敛到局部极小值，难以再减小。下面减少迭代次数为500用于快速获得结果进行观察。

% Init
alpha = 0.1 - 0.001;
num_iters = 500; %50000;
theta = ones(385, 1);
% Run
[theta, J_history] = ...
    gradientDescentMulti(X_train, y_train, theta, alpha, num_iters);

调用的gradientDescentMulti函数用于迭代学习$\theta$，实现如下：

function [theta, J_history] = ...
    gradientDescentMulti(X, y, theta, alpha, num_iters)
%GRADIENTDESCENTMULTI Performs gradient descent to learn theta
% theta = GRADIENTDESCENTMULTI(x, y, theta, alpha, num_iters) updates
% theta by taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
    newDecrement = alpha / m * (X * theta - y)' * X; 
    theta = theta - newDecrement';
    
    % Save the cost J in every iteration   
    % Compute cost for linear regression with multiple variables
    % J_history(iter) = 1 / (2 * m) * sum((X * theta - y).^2);
    J_history(iter) = sqrt(sum((X * theta - y).^2) / m); % RMSE
    fprintf('RMSE: %f \n', J_history(iter));
end
end

需要注意的是，由于Kaggle的评价指标是标准误差(RMSE:Root Mean Squared Error)，默认的代价函数
$$J(\theta_0,\theta_1,…,\theta_n)=\frac{1}{2m}\displaystyle \sum_{ i = 1 }^{ m } (h_\theta(x^{(i)})-y^{(i)})^2$$

1	J_history(iter) = 1 / (2 * m) * sum((X * theta - y).^2);

被改为了
$$J(\theta_0,\theta_1,…,\theta_n)=\sqrt{\frac{\displaystyle \sum_{ i = 1 }^{ m } (h_\theta(x^{(i)})-y^{(i)})^2}{m}}$$

1	J_history(iter) = sqrt(sum((X * theta - y).^2) / m);

对结果没有影响。

交叉验证

在训练集上进行测试是粗糙、不准确的，存在过拟合情况时尤其不可取。一种常用的办法是将训练集的一（小）部分作为验证集，剩下的部分用来训练。验证集和测试集最大的不同是验证集是有标签且可用于调参的，测试集即使有标签也不可用于调参。验证集不能直接被用于训练，但可以根据在验证集上测试的结果调整参数（或模型等）。
交叉验证是多次进行上面的过程，每次选取的验证集不同。例如将训练集分为三份ABC，第一轮A为验证集，BC为新的训练集；第二轮B为验证集，AC为新的训练集；第三轮C为验证集，AB为新的训练集。最后结果为三轮的平均。这样可充分利用数据、减少误差（避免数据不均匀），但同时增加了用时。
下面是进行交叉验证的梯度下降法在MATLAB的实现：

alpha = 0.1 - 0.001;
num_iters = 500;
tic
k = 3;
cv = cvpartition(y_train, 'Kfold', k);
mse = zeros(k, 1);
for k = 1 : k
    trainIdx = cv.training(k);
    testIdx = cv.test(k);
    theta = zeros(385, 1);
    [theta, J_history] = gradientDescentMulti(X_train(trainIdx,:),...
        y_train(trainIdx), theta, alpha, num_iters);
     
    y_hat = X_train(testIdx, :) * theta;
    
    mse(k) = mean((y_train(testIdx) - y_hat).^2);
    fprintf('Fold %d mse: %f \n', k, mse(k));
end
toc
avrg_rmse = mean(sqrt(mse));
fprintf('avrg_rmse: %f \n', avrg_rmse);

结果

将梯度下降迭代的中间结果制图有助于观察收敛情况，选取合适的参数。

% Plot
figure;
plot(1:numel(J_history), J_history, '-b', 'LineWidth', 2); % blue
xlabel('Number of iterations');
ylabel('Cost J');

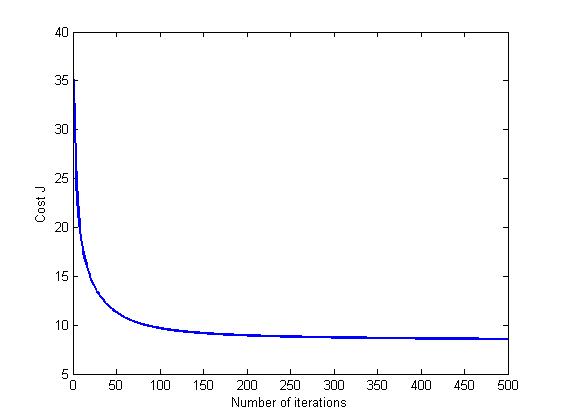
在迭代150次后，收敛速度开始显著下降，迭代500次所用的时间和在训练集上测试的输出为

1
2
3

% ----------- Output -------------
% Elapsed time: 9.203286 seconds
% RMSE on train dataset: 8.562877

交叉验证的输出为：

1
2
3

% ----------- Output -------------
% Elapsed time: 19.245382 seconds
% avrg_rmse: 10.150006

交叉验证的结果往往差于在训练集上测试的结果，与真实测试结果（Kaggle提交score=8.50819）更为接近，可能好/差于真实测试结果。

正规方程(Normal Equation)

Normal equation: Method to solve for $\theta$ analytically which minimize $J$ by
explicitly taking its derivatives with respect to the $\theta_j$’s, and setting them to zero.

算法概观

和梯度下降不同，为了找到代价函数的最小值对应的$\theta$，正规方程法不需要进行多次迭代，而是直接计算极小值点。极小值的计算和计算代价函数上导数为0的点有关。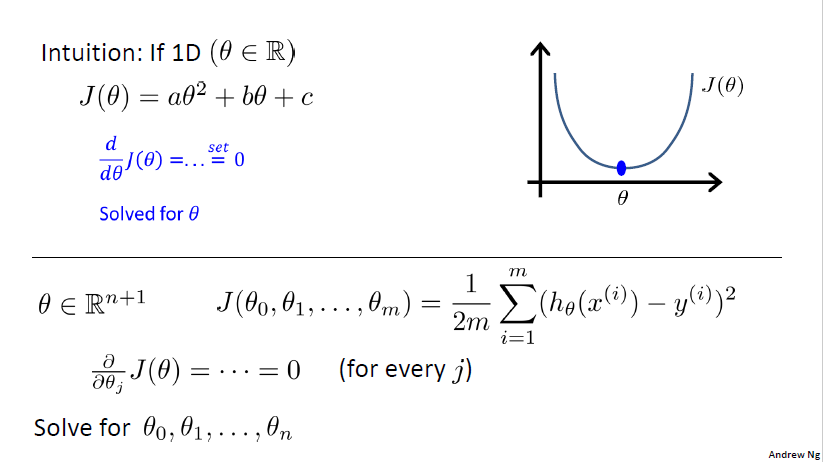

计算参数

$\theta$的计算较复杂，涉及到矩阵的求导、最小二乘法修正，有兴趣的读者请参考CS229 Lecture notes1 Part I - 2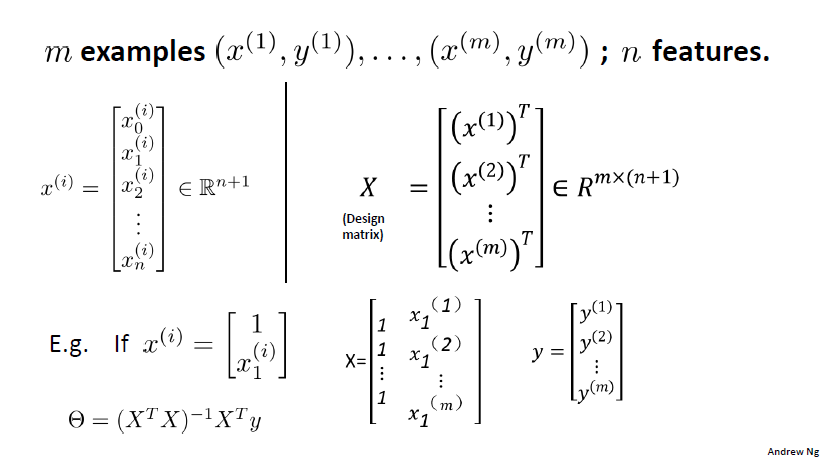

下面提供一种简化的推导：
沿用图六设定的符号，
$$X\theta=y \quad(1)\\
X^TX\theta=X^Ty \quad(2)\\
(X^TX+\lambda I)\theta=X^Ty \quad(3)\\
\theta=(X^TX+\lambda I)^{-1}X^Ty \quad(4)$$
求$\theta$可以转化为求(1)式；(2)式的$X^TX$是$n \times n$矩阵（才可能有逆矩阵）；(3)式的$\lambda$是很小的常数，$I$是单位矩阵，两者相乘得到的矩阵加到$X^TX$上影响可忽略不计，$X^TX+\lambda I$一定有逆矩阵，保证了(4)式的正确性。有两种情况$X^TX$不可逆：

有重复的特征（线性相关）。
特征数过多。

由于这两种情况很少发生，常用下式表示$\theta$：$$\theta=(X^TX)^{-1}X^Ty \quad(4)$$

MATLAB实现

虽然正规方程的推导繁琐，但实现仅需一行代码：

1	theta = pinv(X_train' * X_train) * X_train' * y_train;

MATLAB中的pinv求逆函数处理了X_train' * X_train不可逆的情况，因此不需另外加上$\lambda I$项。
不需要进行特征缩放预处理

交叉验证也很简洁：

k = 3;
cv = cvpartition(y_train, 'Kfold', k);
mse = zeros(k, 1);
for k = 1 : k
    trainIdx = cv.training(k);
    testIdx = cv.test(k);
    theta = pinv(X_train(trainIdx, :)' * X_train(trainIdx, :)) ...
        * X_train(trainIdx, :)' * y_train(trainIdx);
    y_hat = X_train(testIdx, :) * theta;
    
    mse(k) = mean((y_train(testIdx) - y_hat).^2);
    fprintf('Fold %d mse: %f \n', k, mse(k));
end

结果

1
2
3

% ----------- Output -------------
% Elapsed time: 0.368472 seconds
% Normal equation RMSE on train dataset: 8.170871

交叉验证的输出为：

1
2
3

% ----------- Output -------------
% Elapsed time: 1.136081 seconds
% avrg_rmse: 8.325153

Kaggle提交的真实测试结果score=8.44464，可见该例中正规方程法无论是用时还是误差都优于梯度下降法

多层感知器(Multi-layer Perceptron, MLP)

上文中使用了线性回归的方法进行拟合，效果不好，原因可能是数据量大、特征不多，线性模型的表达能力较弱。因此尝试非线性的神经网络。多层感知器是其中最简单的一种。

模型概观

MLP也称为前馈人工神经网络(feedforward neural network)，网络的输入层(input layer)和输出层(output layer)之间有一或多层隐藏层(hidden layer)。前馈意为数据从输入层流向输出层(forward)。这种类型的网络用后向传播(backpropagation)学习算法进行训练的。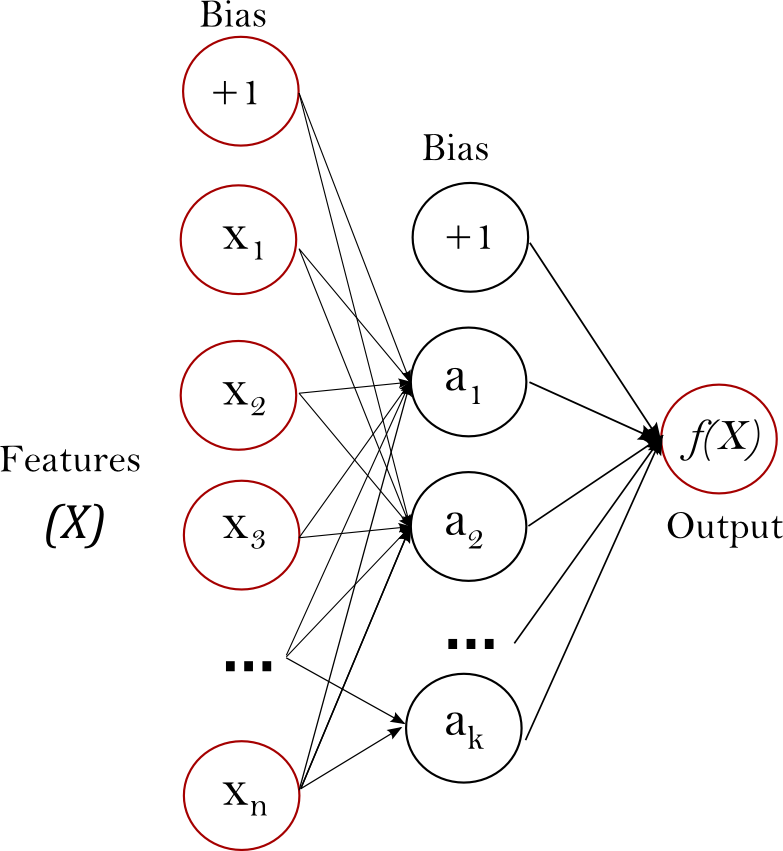

最左边的层即输入层，由一组神经元(neuron)${x_i|x_1,x_2,…,x_m}$代表输入特征。隐藏层中的每个神经元的值通过将前一层中的值通过加权线性求和$w_1x_1+w_2x_2+…+w_mx_m$，再用一个非线性激活函数(non-linear activation function)$g(\cdot):R\rightarrow R$获得。输出层接收上一层的值并转换成输出值。输入输出层均可以有多个神经元。
可以看出多层感知器和线性回归模型最大的区别在于其通过两种方式实现的“非线性”：

非线性激活函数
多层组合

用TensorFlow实现

主框架

下面是用TensorFlow实现(Python语言）多层感知器的主要过程，包含了读写数据、训练、测试，可分为9个步骤(step)：

def main():
    # Step 1: Read data
    print 'Reading training data...'
    train_data_batch, train_label_batch = train_batch_generator([TRAIN_PATH])
    train_features, train_labels = \
            train_generate_batches(train_data_batch, train_label_batch)
    print 'Reading testing data...'
    test_data_batch = test_batch_generator([TEST_PATH])
    test_features = test_generate_batches(test_data_batch)
    # Step 2: create placeholders for features and labels
    with tf.name_scope('data'):
        X = tf.placeholder(tf.float32, [None, 384], name="X_placeholder")
        Y = tf.placeholder(tf.float32, [None, 1], name="Y_placeholder")
    # Step 3: create weight and bias
    w1 = tf.Variable(xavier_init(384, NODE_NUM), name='weights1')
    b1 = tf.Variable(tf.constant(1.0, shape=[NODE_NUM], dtype=tf.float32), name='bias1')
    w2 = tf.Variable(xavier_init(NODE_NUM, NODE_NUM), name='weights2')
    b2 = tf.Variable(tf.constant(1.0, shape=[NODE_NUM], dtype=tf.float32), name='bias2')
    # Step 4: build model to predict Y
    hidden = tf.sigmoid(tf.add(tf.matmul(X, w1), b1))
    Y_predicted = tf.add(tf.matmul(hidden, w2), b2)
    # Step 5: use the square error as the loss function
    loss = tf.reduce_mean(tf.square(Y - Y_predicted), name='loss')
    # Step 6: using gradient descent to minimize loss
    optimizer = \
    tf.train.GradientDescentOptimizer(learning_rate=LEARNING_RATE).minimize(loss)
    # Launch the graph and train
    with tf.Session() as sess:
        # Step 7: initialize the necessary variables, in this case, w and b
        sess.run(tf.global_variables_initializer()) 
    
        writer = tf.summary.FileWriter('./graph', sess.graph)
    
        # Step 8: train the model
        for step in xrange(MAX_STEP):
            # Session runs train_op and fetch values of loss
            _, l = sess.run([optimizer, loss], \
                            feed_dict={X:train_features, Y:train_labels}) 
            print 'Step {0}: loss = {1}'.format(step, np.sqrt(l)) # loss <- RMSE
            
            # Step 9: Test the model every SAVE_ITERS steps
            if (step + 1) % SAVE_ITERS == 0:
                result = sess.run(Y_predicted, feed_dict={X:test_features})
                filename = RESULT_PATH + '_' + str(step) + \
                           '_' + str(int(np.sqrt(l)*100))+ '.csv'
                with open(filename, 'w') as fw:
                    csv_w = csv.writer(fw)
                    csv_w.writerow(['Id', 'reference'])
                    for i in range(BATCH_SIZE):
                        csv_w.writerow([i, result[i][0]])
        # close the writer when you're done using it
        writer.close()

上面的代码对MLP的设置如下：

step 3、step 4定义了MLP的结构：有1个隐藏层，输入层有384（特征数）个神经元，输出层有1个神经元，隐藏层的神经元数为NODE_NUM=50，激活函数为sigmoid
step 6的GradientDescentOptimizer表示用梯度下降法来减少损失，LEARNING_RATE = 0.001
step 8的MAX_STEP=4000：迭代4000步
测试结果（Kaggle提交）score=5.62558，可见非线性模型的拟合能力远优于线性回归（score=8.44464）。

优化

下面在此基础上改进多层感知机以获得更好的结果（每一个改动都在上一个的基础上）。

增加迭代次数MAX_STEP=30000：score=1.77183.

增加隐藏层数为四层如下：score=1.58680.

# Step 3: create weight and bias
w1 = tf.Variable(xavier_init(384, NODE_NUM), name='weights1')
b1 = tf.Variable(tf.constant(1.0, shape=[NODE_NUM], dtype=tf.float32), name='bias1')
w2 = tf.Variable(xavier_init(NODE_NUM, NODE_NUM), name='weights2')
b2 = tf.Variable(tf.constant(1.0, shape=[NODE_NUM], dtype=tf.float32), name='bias2')
w3 = tf.Variable(xavier_init(NODE_NUM, NODE_NUM), name='weights3')
b3 = tf.Variable(tf.constant(1.0, shape=[NODE_NUM], dtype=tf.float32), name='bias3')
w4 = tf.Variable(xavier_init(NODE_NUM, NODE_NUM), name='weights4')
b4 = tf.Variable(tf.constant(1.0, shape=[NODE_NUM], dtype=tf.float32), name='bias4')
w5 = tf.Variable(xavier_init(NODE_NUM, 1), name='weights5')
b5 = tf.Variable(tf.constant(1.0, shape=[1], dtype=tf.float32), name='bias5')
# Step 4: build model to predict Y
hidden = tf.sigmoid(tf.add(tf.matmul(X, w1), b1))
hidden2 = tf.sigmoid(tf.add(tf.matmul(hidden, w2), b2))
hidden3 = tf.sigmoid(tf.add(tf.matmul(hidden2, w3), b3))
hidden4 = tf.sigmoid(tf.add(tf.matmul(hidden3, w4), b4))
Y_predicted = tf.add(tf.matmul(hidden4, w5), b5)

进行三个改动：
- step 4的激活函数改为relu：如
  hidden = tf.nn.relu(tf.add(tf.matmul(X, w1), b1))
- step 6的learning_rate改为动态减小，STARTER_LEARNING_RATE = 1e-2：
  learning_rate = tf.train.exponential_decay(STARTER_LEARNING_RATE, global_step, DECAY_STEPS, DECAY_RATE, staircase=True)
- step 6的optimizer改为AdamOptimizer(区别)：
  optimizer = tf.train.AdamOptimizer(learning_rate).minimize(loss)
  这样的设置下在MAX_STEP=19000时即得到了更优的score=1.15590，说明激活函数relu优于sigmoid，训练过程中改变学习率即可加速收敛又利于达到极小值。
加大隐藏层神经元数NODE_NUM=100，训练MAX_STEP=27000次：score=1.09160.
设置隐藏层神经元数各层不一，分别为300、150、50、10，在MAX_STEP=17000时即得到了更优的：score=0.91748.

可以发现，从score=5.62558到score=0.91748，一开始进步很快，后来举步维艰，已经很难再改进。神经网络迭代次数上万，在多个GPU共同训练的情况下也耗时较多。另一点是调参虽有一定的经验规律可用，但整体还是个黑箱，不容易找到较好的参数。听闻神经网络法在某种繁复的设置下（如采用类似VGG的结构）还是可以达到score~=0.24的，读者有兴趣可进行尝试。

最近邻之scikit-learn

经试验，MLP虽然远优于线性回归，但是也难以获得score<0.5，回头尝试其他传统回归方法。机器学习库scikit-learn已经造了大量轮子，下面介绍用scikit-learn中的最近邻算法及一个trick获得score=0.24633，其他回归方法亦可照葫芦画瓢。

KNN概览

最近邻算法是一种非常直观朴素的算法，对于回归任务，预测一个样本时从特征空间中选择距离该样本最近（最相似）的k个标注样本，该样本的预测值为这些邻居的平均值。如果是分类任务，则预测为大多数邻居所属的类别。
如果采用暴力搜索来找邻居，大数据量下将非常耗时，因此常用一些快速索引结构如Ball Tree或KD Tree。在scikit-learn中只需改algorithm参数即可。
另外“近”可以由不同的标准定义，如欧氏距离、曼哈顿距离；对于不同相近程度的邻居也可以赋予不同的权重或者一视同仁。更多的参数，可参看sklearn.neighbors.KNeighborsRegressor文档

用scikit-learn实现

可参考Nearest Neighbors regression Example(Python语言），下面为主程序代码：

def main():
    # Step 1: Read data
    train_data_batch, train_label_batch = train_batch_generator([TRAIN_PATH])
    train_features, train_labels = \
        train_generate_batches(train_data_batch, train_label_batch)
    test_data_batch = test_batch_generator([TEST_PATH])
    test_features = test_generate_batches(test_data_batch)
    
    # Step 2: Define model
    KNN = neighbors.KNeighborsRegressor(n_neighbors=1)
    # Step 3: Fit the model and predict
    test_labels = knn.fit(train_features, train_labels).predict(test_features)
    
    # Step 4: Write file
    with open('res_nn.csv', 'w') as fw:
        csv_w = csv.writer(fw)
        csv_w.writerow(['Id', 'reference'])
        for i in range(BATCH_SIZE):
            csv_w.writerow([i, test_labels[i][0]])

step 1、step 4是普通的读写数据，和上文MLP所用代码一样。核心的代码只有step 2、step 3的两行，分别用于定义最近邻回归模型和进行训练、预测。n_neighbors默认为5，设置为1可以获得单个最近邻模型的最好结果score=0.26200，相比于MLP获得了突飞猛进的进步。如何找到n_neighbors=1这个“最好”的参数呢？可分割训练集测试。
scikit-learn依然提供了非常方便的方法。在定义了模型之后，可先使用train_test_split方法分割带标注的数据（原训练集）为训练集和测试集，再用fit方法训练，score方法测试获得分数（此处score默认的不是RMSE，但是能反映模型好坏）。

1
2
3

X_train, X_test, y_train, y_test = train_test_split(\
    train_features, train_labels, test_size=0.3, random_state=0)
print knn.fit(X_train, y_train).score(X_test, y_test)

在训练集数据量不是很大或者想获得更均匀准确的估测结果的情况下，可以使用交叉验证（缺点是耗时相对长）：

1
2
3

scores = cross_val_score(knn, train_features, train_labels, \
    cv=10, scoring='neg_mean_squared_error')
print (scores, np.sqrt(np.abs(scores.mean()))) # RMSE

Trick

从提交结果看，nn(k=1)和2nn(k=2)的结果最好，相差0.01.下面采用的Trick姑且称为杂交优势：

knn	2nn	nn	$0.5nn+0.52nn$	$0.6nn+0.42nn$
score	0.27622	0.26200	0.24697	0.24635

这种方法确实有偶然性，但也是有依据的：赋予不同距离的邻居不同的权重。设最近的邻居为$f$，第二近的邻居为$s$，由于前面采用的是默认的weights='uniform'即全部邻居全部相同权重，可以看做$2nn=(f+s)*0.5$，因此下面这个例子可以拆分成
$$0.6*nn+0.4*2nn=0.6*(f)+0.4*(f+s)*0.5=0.8*f+0.2*s$$ 也就是以4:1的权重来对待$f$和$s$，相当于自定义了weights.

其实，这种方法可视为ensembling方法中最简单的一种，具体请参考KAGGLE ENSEMBLING GUIDE。

各回归方法对比

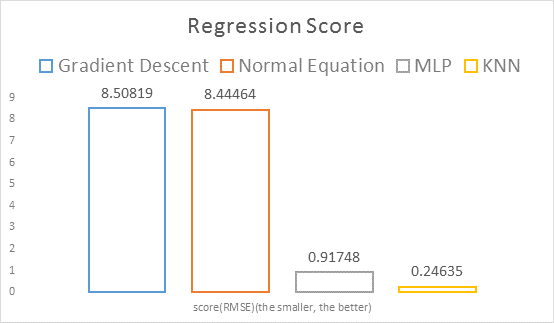
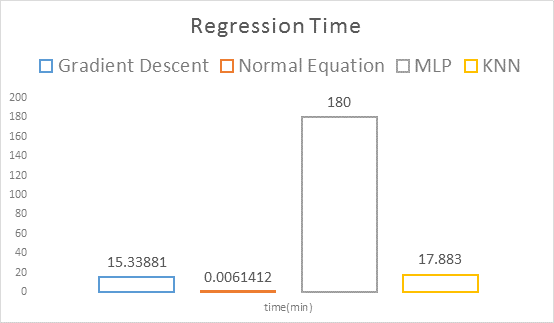
结论：线性回归方法误差过高，淘汰；KNN又快又准，胜出；神经网络再接再厉，兴可推前浪。

分类(Classification)

Identifying to which category (discrete labels) an object belongs to.

分类预测的是离散的值（类别）。
Kaggle link: Large-scale classification-SYSU-2017

该例中是二分类问题，$y\in \{0,1\}$

数据(Data)

1.train_data.txt
The format of each line is label index1:value1 index2:value2 index4:value4 ... where value1,value2,… are the features(the ignored value equals 0 e.g. the value3 here equals 0) and there are only 2 classes(label) in all,indexed from 0 to 1.
2.test_data.txt
This file contains the features without labels that you need to predict. The format of each line is id index1:value1 index2:value2 index3:value3 ...
3.sample_submission.txt (or result.txt)
The file you submit should have the same format as this file,the format of each line is id,label

度量标准(Evaluation)

AUC(Area under Receiver Operating Characteristic Curve)[binary-classification]
越大越好

逻辑回归(Logistic Regression)

推荐阅读：CS229 Lecture notes1 Part II

逻辑“回归”是用于分类任务而非回归任务的。

Hypothesis Representation

联想一开头讨论的线性回归算法，求解分类问题可以先忽视$y$是离散值，而套用线性回归算法给定$x$预测$y$.此思路最大的问题在于预测的连续值大于1或小于0时都无意义，因为$y\in \{0,1\}$.然而，通过逻辑函数(logistic function)（或sigmoid函数），可以将范围限制在0和1之间：
$$h_{\theta}(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}},\\
where \quad g(z)=\frac{1}{1+e^{-z}},\\
\theta^Tx=\theta_0+\sum_{ j = 1 }^{ n } \theta_jx_j$$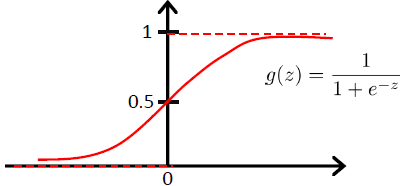

其他能将值平滑映射为从0增加到1的函数也可，sigmoid函数直观简单，它的导数也有着很好的形式：
$$
\begin{eqnarray}
g’(z) &=& \frac{d}{dz} \frac{1}{1+e^{-z}}\\
&=& \frac{1}{(1+e^{-z})^2}(e^{-z})\\
&=& \frac{1}{(1+e^{-z})} \cdot (1-\frac{1}{(1+e^{-z})})\\
&=& g(z)(1-g(z))
\end{eqnarray}
$$

梯度上升法

Likelihood of the Parameters

假设
$$\begin{eqnarray}
P(y=1|x;\theta)&=&h_{\theta}(x)\\
P(y=0|x;\theta)&=&1-h_{\theta}(x)
\end{eqnarray}$$

$P$是概率/可能性(likelihood)，我们的目标是最大化$P$。因为假设在$P$最大的边界情况下$P=1$，根据假设：

当一个样本的真实标签$y=1$时，这个样本的预测值$h_{\theta}(x)=1$，预测正确；
当一个样本的真实标签$y=0$时，这个样本的预测值$h_{\theta}(x)=0$，预测正确。

接下来皆使用一个更简洁的式子来代替上面两个式子的表示：
$$P(y|x;\theta)=(h_{\theta}(x))^y(1-h_{\theta}(x))^{1-y}$$

假设m个训练样本各自独立生成，从而可以统一表示所有参数的这种可能性(the likelihood of the parameters)：

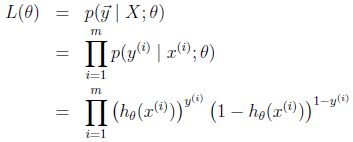
Maximize the Likelihood (Gradient Ascent)

首先对$L(\theta)$做对数运算，这样有利于求最大值
$$\begin{eqnarray}
l(\theta) &=& \log L(\theta)\\
&=& \sum_{i=1}^{m} y^{(i)}\log h(x^{(i)})+(1-y^{(i)})\log (1-h(x^{(i)}))
\end{eqnarray}$$

和线性回归的求解思路（梯度上升法）相似，下面采用梯度上升法来最大化(likelihood)函数，更新规则如下：
$$\theta:=\theta+\alpha {\nabla}_{\theta} l(\theta)$$
(用正号而非符号是因为此时我们需要最大化而非最小化函数，更多相关解释，可回到上文的梯度“上升”的含义)

以一个样本$(x,y)$为例展开求导（利用了前面推导的sigmoid函数的导数$g’(z)=g(z)(1-g(z))$和$(lnx)’=1/x$）：

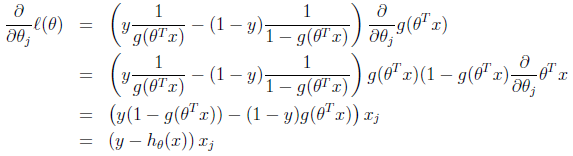
求得随机梯度上升规则
$$\theta_j:=\theta_j+\alpha (y^{(i)}-h_{\theta}(x^{(i)})) x_j^{(i)}$$

上式看起来和线性回归的求解方法随机梯度下降（和梯度下降的不同是每次更新是随机选一个样本而非全部样本）的更新规则看起来完全一样：

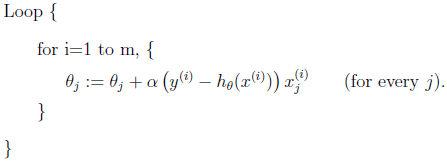
但它们不是同一个算法，因为在随机梯度上升规则中的$h_{\theta}(x^{(i)})$是$\theta^Tx^{(i)}$的非线性函数，而线性回归中的是线性的。
尽管如此，两者形式上的相同并不是巧合，它们有更深层次的联系（Generalized Linear Models），感兴趣的读者可阅读CS229 Lecture notes1 Part III.

梯度下降法

上文所讨论的梯度上升法针对的是最大化$l(\theta)$，是正式完整的逻辑回归求解过程。下面讨论梯度下降法，针对最小化代价函数。两者实质是一样的，或者说，梯度下降法优化的代价函数的表示可以（可能就是）从$l(\theta)$得来的。
算法如下：

$J(\theta)$表示代价函数，它在上文推导出的$l(\theta)$基础上乘一个负数$-\frac{1}{m}$将原来最大化的问题转化为最小化，这种转化是因为我们总是最小化代价函数（代价小）。在此基础上可以求导、迭代等，和线性回归中梯度下降的过程类似。

梯度法分类及实现

下面以逻辑回归的梯度上升法为例，用Python语言分别实现批量梯度上升、随机梯度上升、小批量梯度上升法及批量梯度上升法的多进程并行化。
前文已经讨论过，逻辑回归的梯度上升法和梯度下降法实质是一样的，具体来说，下面代码（梯度上升）中的：

1
2
3

error = labelMat[i] - sigmoid(predict(weights, data))
for d in data:
    _weights[d] = _weights[d] + alpha*error*data[d]

两行各换个符号便是梯度下降法了，实际相同：

1
2
3

error = sigmoid(predict(t_weights, data)) - labelMat[i]
for d in data:
    _weights[d] = _weights[d] - alpha*error*data[d]

数据预处理

使用梯度法需要将数据进行特征缩放(feature scaling)！经测试，该步骤非常必要。后面的实现测试中，若未进行特征缩放，准确率总是为45%（比瞎猜还差），进行特征缩放后，第一次迭代的准确率即可超过50%.

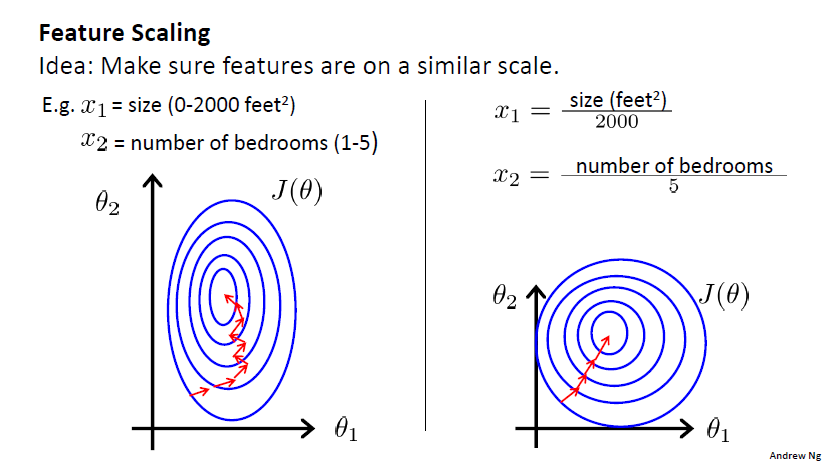
特征缩放作用的简化直观理解可参见上图。
本例中我使用了$\frac{x-min}{max-min}$对每个特征的值(x)进行处理，min和max分别是最小值和最大值。
值得注意的是，训练集和测试集都需要进行同样尺度的特征缩放。具体做法是先找到训练集的min,max，对训练集和测试集都用这个min,max缩放。
该例中的数据有一些异常：训练集的特征的index范围有1-201，测试集只有1-132.因此可预处理将训练集特征的index大于133的去除
训练集/测试集的样本从某一行开始重复（具体忘了，若要用此数据，可除重）

批量梯度上升法(Batch Gradient Ascent)

前面我们讨论的公式几乎都是批量梯度上升法，每采取一步更新都需要遍历全部训练集样本。当样本数较大时，成本较高。

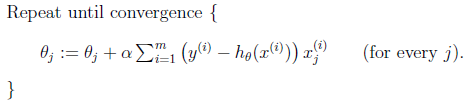
实现时要注意：

权重（参数$\theta$）随机初始化的效果优于固定值初始化
在每次迭代要同步更新权重，因此需要先拷贝原权重用于该次迭代所有需更新的权重的计算，以免先计算的某个权重被用于其他权重的计算导致其他权重的计算是“后更新”的。（绕，看代码）

def batchGradAscent(dataMat, labelMat, valDataMat, valLabelMat, numIter = N_ITER):
    alpha = ALPHA
    weights = [random.random() for i in range(N_FEATURE + 1)] # random init
    totalTime = 0.0
    for iter in range(numIter):
        start = time.time()
        _weights = [weights[i] for i in range(N_FEATURE + 1)] # copy
        for i in range(len(dataMat)):
            dataDict = parseData(dataMat[i])
            error = labelMat[i] - sigmoid(predict(weights, dataDict))
            for index in dataDict:
                _weights[index] = _weights[index] + alpha*error*dataDict[index]
        weights = [_weights[i] for i in range(N_FEATURE + 1)] # update
        end = time.time()
        totalTime = totalTime + float(end - start)
        calcAcc(weights, valDataMat, valLabelMat, iter)
    print 'batchGradAscent iter cost:', float(totalTime) / numIter, 's in average.'
    return weights

随机梯度上升法(Stochastic Gradient Ascent)

随机梯度上升法重复遍历训练集，每次遇到一个训练样本，都只根据和这一个训练样本相关的误差梯度(the gradient of the error)来更新参数。在训练集样本多的情况下，这种方法大大减小了计算成本，加快了收敛速度（但有可能永远收敛不到最小值而是一直在最小值周围震荡）。

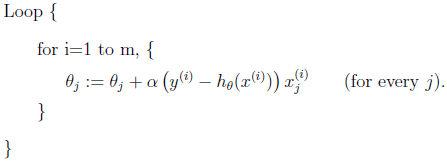
实现时要注意：

该实现随机选取一个样本
该实现每次迭代随机采样的次数等于训练样本数（即公式中的m），这样在每次迭代中可随到大多数样本，样本丰富性高。如需加速，可减小采样数。

def stocGradAscent(dataMat, labelMat, valDataMat, valLabelMat, numIter = N_ITER):
    alpha = ALPHA
    weights = [random.random() for i in range(N_FEATURE + 1)]
    totalTime = 0.0
    for iter in range(numIter):
        start = time.time()
        for i in range(len(dataMat)):
            randIndex = int(random.uniform(0,len(dataMat)))
            dataDict = parseData(dataMat[randIndex])
            error = labelMat[randIndex] - sigmoid(predict(weights, dataDict))
            for index in dataDict:
                weights[index] = weights[index] + alpha*error*dataDict[index]
        end = time.time()
        totalTime = totalTime + float(end - start)
        calcAcc(weights, valDataMat, valLabelMat, iter)
    print 'stocGradAscent iter cost:', float(totalTime) / numIter, 's in average.'
    return weights

小批量梯度上升法(Mini-batch Gradient Descent)

这是批量梯度上升法和随机梯度上升法的折中方案。每次迭代随机选取n个样本更新参数。
实现时要注意：

小批量的选取样本数大于1，每次迭代仍需同时更新参数，需要拷贝参数。
为了有较高的样本覆盖率，下面实现中设定每次迭代随机采样的次数为：$\frac{总训练样本数}{单批量数}$

def minibatchGradAscent(dataMat, labelMat, valDataMat, valLabelMat,\
 batch = 10, numIter = N_ITER):
    alpha = ALPHA
    weights = [random.random() for i in range(N_FEATURE + 1)]
    totalTime = 0.0
    for iter in range(numIter):
        start = time.time()
        for j in range(len(dataMat) / batch):
            randIndex = int(random.uniform(0,len(dataMat)-batch))
            _weights = [weights[i] for i in range(N_FEATURE + 1)]
            for i in range(batch):
                dataDict = parseData(dataMat[randIndex+i])
                error = labelMat[randIndex+i] - sigmoid(predict(weights, dataDict))
                for index in dataDict:
                    _weights[index] = _weights[index] + alpha*error*dataDict[index]
            weights = [_weights[i] for i in range(N_FEATURE + 1)]
        end = time.time()
        totalTime = totalTime + float(end - start)
        calcAcc(weights, valDataMat, valLabelMat, iter)
    print 'minibatchGradAscent iter cost:', float(totalTime) / numIter, 's in average.'
    return weights

并行化

使用Python的多进程对逻辑回归的批量梯度上升法中计算梯度的过程进行并行化，达到加速运算的目的。

选择方法

选择批量梯度上升法是因为每次迭代整个训练集都要计算梯度，但又互不影响，没有依赖关系和数据访问冲突问题。最终参数的更新在全部样本完成梯度计算之后进行汇合。

首先，要清楚所使用机器和并行化相关的配置，如在Linux系统中可通过lscpu命令查看和CPU架构相关的信息，了解核数、CPU数等。

[root@localhost ~]$ lscpu
Architecture:          x86_64
CPU op-mode(s):        32-bit, 64-bit
Byte Order:            Little Endian
CPU(s):                72               # 一个核可以包含多个CPU
On-line CPU(s) list:   0-71
Thread(s) per core:    2                # 每个CPU核支持两个线程（超线程）
Core(s) per socket:    18               # 一个socket可以包含多个核
Socket(s):             2                # 共有两个socket
NUMA node(s):          2
Vendor ID:             GenuineIntel
CPU family:            6
Model:                 79
Model name:            Intel(R) Xeon(R) CPU E5-2695 v4 @ 2.10GHz
# 省略了部分输出

或者使用更具体的命令查看Linux物理CPU个数、核数、逻辑CPU个数：

# 总核数 = 物理CPU个数 X 每个物理CPU的核数
# 总逻辑CPU数 = 物理CPU个数 X 每颗物理CPU的核数 X 超线程数
$ cat /proc/cpuinfo| grep "physical id"| sort| uniq| wc -l
2                    # 物理CPU个数为2
$ cat /proc/cpuinfo| grep "cpu cores"| uniq
cpu cores   : 18     # 每个物理CPU中core的个数(即核数)为18
$ cat /proc/cpuinfo| grep "processor"| wc -l
72                   # 逻辑CPU的个数为72

该服务器核数较多。

选择多进程而非多线程和Python并行化机制有关。有一个较为普遍的认识：

python中的多线程其实并不是真正的多线程，如果想要充分地使用多核CPU的资源，在python中大部分情况需要使用多进程。（Python多进程编程）

由于本例中逻辑回归使用Python编程，且所使用的服务器十分符合多核CPU，Python还提供了好用的多进程包multiprocessing，本例采用Python多进程来对逻辑回归的批量梯度上升法进行并行化。
进一步参考为什么在Python里推荐使用多进程而不是多线程？，在Python多线程下，每个线程的执行方式是
1). 获取GIL(Global Interpreter Lock全局解释器锁)
2). 执行代码直到sleep或者是python虚拟机将其挂起。
3). 释放GIL

也就是说，进入CPU执行代码需要获得GIL，而在一个Python进程中，GIL只有一个，即使一个进程中有多线程也只有获得GIL的线程才能执行。非但如此，在释放GIL时的线程锁竞争、切换线程的会消耗资源。
而多进程的好处在于，每个进程有各自独立的GIL，互不干扰，利于并行执行，所以在python中，多进程的执行效率优于多线程(仅仅针对多核CPU而言)。

实现多进程

multiprocessing是Python的多进程包，支持子进程、通信和数据共享，提供了Process、Queue、Pipe、Lock等组件。下面将用到的是Process，类和方法如下：

创建进程的类：Process([group [, target [, name [, args [, kwargs]]]]])
target表示调用对象，args表示调用对象的位置参数元组。kwargs表示调用对象的字典。name为别名。group实质上不使用。
方法：is_alive()、join([timeout])、run()、start()、terminate()
其中，Process以start()启动某个进程。

下面是主程序。和原批量梯度上升法实现的主要区别在于代码中间部分用到的Process类。target=func中的func是自定义函数，用于指定每个进程的任务，在该例中为calcGrad，即计算一部分样本梯度。process通过start()、join()等方法控制进程的开始、汇合。代码中还用到了Lock()，在多个进程需要访问共享资源weights时可以避免访问冲突。

def batchGradAscentMultiProcess(dataMat, labelMat, valDataMat, valLabelMat, \
    processNum = 18, numIter = N_ITER):
    _weights = Array('f', range(N_FEATURE + 1))
    alpha = ALPHA
    weights = [random.random() for i in range(N_FEATURE + 1)] # random init
    
    sampleNum = len(dataMat)
    if sampleNum < processNum:
        processNum = sampleNum
    step = sampleNum / processNum # workload of each process
    
    totalTime = 0.0
    for iter in range(numIter):
        start = time.time()
        lock = Lock()
        for i in range(len(weights)): _weights[i] = weights[i]
        processes = [] # list
        for i in range(0, sampleNum, step):
            if i + step > sampleNum:
                continue
            process = Process(target=calcGrad, \
                args=(_weights, alpha, dataMat[i:i+step], labelMat[i:i+step], lock))
            processes.append(process)
        for i in range(len(processes)):
            # print 'Process ', i, ' started.'
            processes[i].start()
        # join(): Block the calling thread until the process
        # whose join() method is called terminates
        for i in range(len(processes)):
            processes[i].join()
            # print 'Process ', i, 'ended.'
        weights = [_weights[i] for i in range(N_FEATURE + 1)]
        end = time.time()
        totalTime = totalTime + float(end - start)
        calcAcc(weights, valDataMat, valLabelMat, iter)
    print 'batchGradAscentMultiProcess iter cost:', float(totalTime) / numIter,\
    's in average. processNum:', processNum
    return weights

calcGrad计算梯度在非并行化版本上加了两个步骤：

_weights是共享变量，t_weights是_weights的拷贝，先对t_weights进行各种操作，最后通过加锁来更新共享变量。由于多进程共享资源会引起进程间相互竞争，通过这种“拷贝”将复杂的操作转移到非共享变量上可以减少竞争对结果的不确定性影响。
更新共享变量前需加锁：with lock

def calcGrad(_weights, alpha, dataMat, labelMat, lock):
    t_weights = [_weights[i] for i in range(N_FEATURE + 1)]
    sums = [0 for i in range(N_FEATURE + 1)]
    for i in range(len(dataMat)):
        data = parseData(dataMat[i])
        error = labelMat[i] - sigmoid(predict(t_weights, data))
        for d in data:
            sums[d] = sums[d] + alpha*error*data[d]
    with lock:
        for i in range(N_FEATURE + 1):
            _weights[i] += sums[i]

并行效果

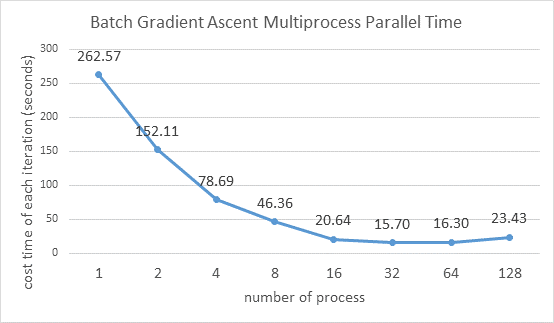
现象：

进程数从1以两倍的关系递增到16的过程中用时基本呈减半关系下降
16进程到32进程的用时减少，但幅度不大
32进程左右再增大进程数不仅没有减少用时，反而略微增加了。

解释：

符合预期，成功实现多进程并行化
进程数较多时，每个进程计算梯度的用时很小，那些用于构建并行化操作的基础用时（如start、join、lock）在总用时中的比重变大，变得可见。
所用服务器的总核数（不是逻辑总核数，多进程不计超线程的影响）是36，与32接近，能开启的进程数已饱和（服务器上的部分CPU也在进行别的任务）。反而增加了用时（猜测）是因为做了无用功。

并行化和其他非并行化方法的对比，请见下文

结果及比较

结果

使用逻辑回归之梯度上升法训练约50次（$\alpha=0.01）便难以再提升，预测出的label在0.5上下，因此直接四舍五入成0和1，提交结果score = 0.72512.后面将介绍的XGBoost的效果大幅(score > 0.9)超越逻辑回归，因此不再继续对逻辑回归调参，仅作为一个方法比较。

准确率比较

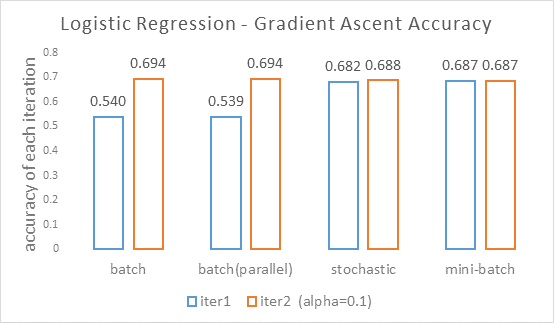
上图是设$\alpha=0.1$设各方法迭代两次统计的准确率，准确率的计算方法是预测值大于等于0且标签为1或预测值小于0且标签为0时预测正确。该学习率设置得较大是为了使在两次迭代（节省运行时间）情况下就可以看出准确率的变化。
测试结果在一定程度上表现了

并行化和非并行化版本的结果一致，说明实现过程是正确的。
随机梯度上升法和小批量梯度上升法均在第一次迭代就获得了较批量梯度上升法高许多的准确率，说明前者较后者“前进步伐”更大。
随机梯度上升法和小批量梯度上升法第二次迭代的准确率较第一次几乎没有变化，这（可能）是因为学习率过大，导致在极小值附近“震荡”。
批量梯度上升法在第二次迭代取得了长足的进步。

用时比较

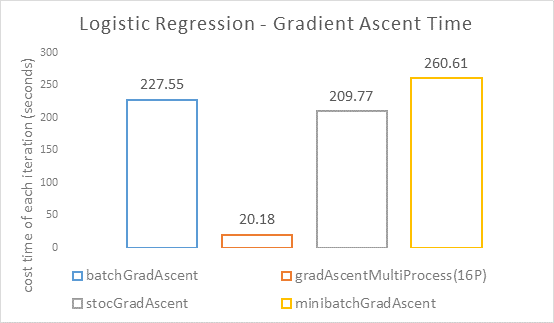
上图是四种方法单次迭代（由两次迭代用时平均得来）所用时间的比较。注意计时时不考虑测试准确率的用时（因为未对这个操作进行并行化，计入会影响并行化时间比较），但考虑了除此之外单次迭代中所用到的各种操作，包括复制权重、并行化的进程相关操作等。
测试结果在一定程度上表现了

16进程并行化的批量梯度上升法无疑是最快速的，但未达到16倍的加速（约11倍），这与多进程需要额外的操作有关（如等待各子进程完成梯度计算才能更新权重）。
根据前面非并行化三种方法的实现可知，这三种方法都用了同样多次数的循环操作（迭代次数*总训练样本数），最终三者时间上仍有一定差异。

GBDT之XGBoost

除了逻辑回归法，还有很多方法（例如梯度提升决策树GBDT）可用于分类，且效果往往更佳。和scikit-learn类似，XGBoost (eXtreme Gradient Boosting)也是造轮子的，使用较为简便。通过一个官方的二分类例子XGBoost demo: binary classification，即可上手（安装配置XGBoost可能相对耗时）。
最简单的使用方法如demo所示，不需要写代码，只需更改.conf文件中的参数设置，参考.sh文件中的命令运行即可。在默认的参数设置下都可取得不错（score>0.9，远优于逻辑回归）的结果。但是要想大幅改进，就不得不开始调参再调参（以及可结合scikit-learn利用交叉验证等等）。

输入数据格式

XGBoost使用的是LibSVM格式，样例如下

1
2
3

1 101:1.2 102:0.03
0 1:2.1 10001:300 10002:400
...

每行代表一个样本，第一列是标签（类别），诸如101:1.2格式的表示第101号特征值为1.2.以此类推。
分类比赛的Kaggle数据集格式和XGBoost的要求不谋而合，因此无需改动数据格式。

一般操作

安装完成后，在xgboost文件夹下有一个xgboost文件，假设其绝对路径为/home/xgboost/xgboost.

.conf文件是用来指定各种参数的，可以放在任意路径下，假设当前路径在classification.conf目录下。classification.conf文件如下：

# General Parameters, see comment for each definition
# can be gbtree or gblinear
booster = gbtree
# choose logistic regression loss function for binary classification
objective = binary:logistic
# Tree Booster Parameters
# step size shrinkage
eta = 0.01
# minimum loss reduction required to make a further partition
gamma = 0
# minimum sum of instance weight(hessian) needed in a child
min_child_weight = 7
# maximum depth of a tree
max_depth = 12
# Task Parameters
# the number of round to do boosting
num_round = 1000
# 0 means do not save any model except the final round model
save_period = 100
# set evaluation metric
eval_metric = auc
# The path of training data
data = "train10_9.txt"
# data = "train_data.txt"
# The path of validation data, used to monitor training process, 
# here [val] sets name of the validation set
eval[val] = "val10_1.txt"
# eval[train_full] = "train_data.txt"
# The path of test data
test:data = "test_data.txt"
model_dir="models_etad01_ga0_mcw7_dep12"

当前设置下的data = "train10_9.txt"和eval[val] = "val10_1.txt"是将完整的带标签的数据集以9:1比例分成了训练集和验证集用于调参，真正测试时需要改为data = "train_data.txt"来训练。在我的设置中，model_dir="models_full_etad01_ga0_mcw7_dep12"用于指定生成模型的路径，文件名和设定的提升树参数(Tree Booster Parameters)一致，运行前需要先创建该目录。

常用的运行命令如下：

#!/bin/bash
# training and output the models
nohup /home/xgboost/xgboost classification.conf >> models_etad005_ga0_mcw9_dep12/nohup.out 2>&1 &
# Continue from Existing Model
nohup /home/xgboost/xgboost classification.conf model_in=/home/classification/models_etad01_ga0_mcw7_dep12/0900.model num_round=100 model_out=1000.model >> models_etad01_ga0_mcw7_dep12/nohup.out 2>&1 &
# output prediction task=pred 
/home/xgboost/xgboost classification.conf task=pred model_in=/home/classification/models_etad01_ga0_mcw7_dep12/0800.model

注意上面命令不需要同时使用，使用时把不需要的注释掉。

训练：用nohup后台训练并将输出内容存到模型文件夹下的nohup.out中
继续训练：在已有模型0900.model基础上再训练100步
预测：用模型0800.model进行预测

调参(Parameter Tuning)

参数主要分为三类：一般参数(General Parameters)、提树参数(Tree Booster Parameters)、任务参数(Task Parameters)，我们主要调节的是Tree Booster Parameters.调参方法具体可参考Complete Guide to Parameter Tuning in XGBoost (with codes in Python).
一般来说分为以下几步：

选择一个相对高的eta（一般可选0.1），在此基础上找到最优的max_depth.
在上一步基础上找到最优的min_child_weight
在上一步基础上找到最优的gamma
减小eta，加大max_depth训练。

Reference & Futher Reading