[CVPR] A4 Paper Sheet Detection and Cropping with Hough Transform and Warping

Function similar to Document Scanner. Given images of A4 paper sheets, output paper sheets’ four corners as well as four edges and their equations. Then crop the background and leave the paper sheet in proper position and standard scaling. We can do this in three steps. Firstly, detect edges with hough transform. Then store the corners in order. Lastly, applying a perspective transform to warp the image.

★Source codes and images here

Here’s a Document Scanner tutorial implemented with OpenCV(without all theory details).

Edge Detection with Hough Transform

★Here’s an excellent c++ example part of the CImg Library project: Computation of the Hough Transform Illustrate the computation of the Hough transform to detect lines in 2D images. Provide also simple user interface to select and display lines

Theory

The purpose of the Hough transform is to address this problem by making it possible to perform groupings of edge points into object candidates by performing an explicit voting procedure over a set of parameterized image objects (Shapiro and Stockman, 304).

Reference: wiki

The Hough transform is a feature extraction technique. The simplest case of Hough transform is detecting straight lines. In general, the straight line $y = mx + b$ can be represented as a point $(b, m)$ in the parameter space. However, vertical lines pose a problem. They would give rise to unbounded values of the slope parameter m. Thus, for computational reasons, Duda and Hart[5] proposed the use of the Hesse normal form

$$rho = x\cos \theta + y\sin \theta$$

where $r$ is the distance from the origin to the closest point on the straight line, and $\theta$ is the angle between the $x$ axis and the line connecting the origin with that closest point.

Even if lines are not vertical, parameter $m$ and $b$ can get rather large which is hard to define their bounds. The transform is necessary.

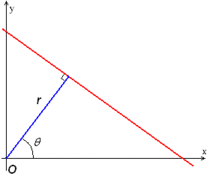
It is therefore possible to associate with each line of the image a pair $(r,\theta )$. The $(r,\theta )$ plane is sometimes referred to as Hough space for the set of straight lines in two dimensions.

Given a single point in the plane, then the set of all straight lines going through that point corresponds to a sinusoidal curve in the $(r,\theta )$ plane, which is unique to that point. A set of two or more points that form a straight line will produce sinusoids which cross at the $(r,\theta )$ for that line. Thus, the problem of detecting collinear points can be converted to the problem of finding concurrent curves.

Also see: MathWorks: hough.

Implementation

Note: the codes has been updated (improved) in GitHub.

Reference: Leo’s blog

Init

The hough_space is a parameter space matrix whose columns and rows correspond to $angle$ and $rho$ values respectively. Its width range represents the possible degrees of each angle of the straight line passing through a point. Its height range represents the largest possible of $rho$ which is the distance of two diagonal corners in image.

rgb_img.load_bmp(filePath);
w = rgb_img.width();
h = rgb_img.height();
gray_img = gradients = CImg<double>(w, h, 1, 1, 0);
hough_space = CImg<double>(360, distance(w, h), 1, 1, 0);

Pre-treatment

• Convert rgb image to grayscale image because the color information helps little here.
• Blur the grayscale image helps a lot in noise reduction and focusing on the real edges.
• Get intensity gradient magnitude of grayscale image for edge detection. For each pixel in grayscale image, it’s intensity gradient magnitude is calculated by $\sqrt{gradX^2 + gradY^2}$. I use one dimensional filter (next pixel value minus previous pixel value in x-axis and y-axis for $gradX$ and $gradY$ respectively).

rgb2gray();
gray_img.blur(BLUR_SIGMA); // noise reduction
getGradient();

/* Euclidean distance / Pythagorean Theorem */
double Hough::distance(double diff_x, double diff_y) {
    return sqrt(diff_x * diff_x + diff_y * diff_y);
}

/* RGB to grayscale transformation */
void Hough::rgb2gray() {
    cimg_forXY(rgb_img, x, y) {
        int r = rgb_img(x, y, 0);
        int g = rgb_img(x, y, 1);
        int b = rgb_img(x, y, 2);
        gray_img(x, y) = 0.299 * r + 0.587 * g + 0.114 * b;
    }
}

/* get intensity gradient magnitude for edge detection */
void Hough::getGradient() {
    CImg_3x3(I, double);
    cimg_for3x3(gray_img, x, y, 0, 0, I, double) {
        // one-dimension filter better than 2D(sobel etc)
        gradients(x, y) = distance(Inc - Ipc, Icp - Icn);
    }
}

CImg function usage: Using Image Loops
CImg_3x3(I,type) : Define a 3x3 neighborhood named I, of type type. Actually, I is a generic name for the neighborhood. In fact, these macros declare a set of new variables.

For instance, defining a 3x3 neighborhood CImg_3x3(I,float) declares 9 different float variables Ipp,Icp,Inp,Ipc,Icc,Inc,Ipn,Icn,Inn which correspond to each pixel value of a 3x3 neighborhood. Variable indices are p,c or n, and stand respectively for ‘previous’, ‘current’ and ‘next’. First indice denotes the x-axis, second indice denotes the y-axis. Then, the names of the variables are directly related to the position of the corresponding pixels in the neighborhood.

• Ipp = img(x-1,y-1)
• Icn = img(x,y+1)
• Inp = img(x+1,y-1)

cimg_for3x3x3(img,x,y,z,c,I,T) : Loop along the (x,y,z)-axes using a centered 3x3x3 neighborhood.

Transform to Hough Space

The elements in the hough_space represent accumulator cells. Initially, the value in each cell is zero. Then, for each pixel at $(x,y)$ with strong gradient (larger than GRAD_THRESHOLD), $rho$ is calculated for every $angle$ between 0 and 360 degrees, and $rho$ is calculated for every $theta$. $rho$ is rounded off to the nearest allowed row in hough_space.

If $rho$ is valid, we look for the accumulator’s bin that the parameters $(angle,rho)$ fall into, and increment the value of that bin.

At the end of this procedure, a value of $Q$ in hough_space(a, r) means that $Q$ points in the xy-plane lie on the line specified by $angle(a)$ and $rho(r)$. Peak values in the hough_space represent potential lines in the input image.

/* Transform points in parameter space to hough space */
void Hough::houghTransform() {
    cimg_forXY(gradients, x, y) {
        // consider only strong edges, 
        // also helps to reduce the number of votes
        if (gradients(x, y) > GRAD_THRESHOLD) {
            cimg_forX(hough_space, angle) {
                double theta = 1.0 * angle * cimg::PI / 180.0;
                int rho = (int)(x*cos(theta) + y*sin(theta));
                if (rho >= 0 && rho < hough_space.height())
                    ++hough_space(angle, rho);
            }
        }
    }
}

Looking for Local Maxima in Hough Space

By finding the bins with the highest values, typically by looking for local maxima in the accumulator space, the most likely lines can be extracted, and their (approximate) geometric definitions read off. (Shapiro and Stockman, 304)

In order to find these peaks, I apply threshold of the form (modify from this paper)

$$floor(maxVal/Q)$$

maxVal is the max value in the accumulator space hough_space, Q is used to adjust threshold. In the paper, $Q=\sqrt 2$, but I set $Q=3$ in my code so that more than three local maxima can be filtered out in all test images. It’s fine that more than 4 local maxima are filtered out because we can easily pick the four brighest(largest pixel value) points which correspond to four edges of a paper sheet.
By setting value in hough_space smaller than threshold to zero(black) we can clearly see how many local maxima are filtered out.

By the way, a good form of threshold saves you from adjusting parameters for each image.

/* Compare function for HoughEdge sort.
The strongest edge rank first. */
bool cmp_edges(HoughEdge e1, HoughEdge e2) {
    return e1.val > e2.val;
}

/* Find out four edges of paper sheet in parameter space 
*  => Get four clusters with the highest values and 
*  select the brighest point from each of them.
*/
void Hough::getHoughEdges() {
    int maxVal = hough_space.max();
    int threshold = floor(maxVal / Q);
    std::cout << maxVal << " " << threshold << std::endl;
    cimg_forXY(hough_space, angle, rho) {
        int val = hough_space(angle, rho);
        if (val < threshold) {
            hough_space(angle, rho) = 0;
        }
        else {
            HoughEdge hough_edge(angle, rho, val);
            bool is_new_corner = true;
            for (int i = 0; i < hough_edges.size(); ++i) {
                if (distance(hough_edges[i].angle - angle,
                    hough_edges[i].rho - rho) < SCOPE) {
                    is_new_corner = false;
                    // compare with the other value in this cluster
                    if (val > hough_edges[i].val) {
                        hough_edges[i] = hough_edge; // update
                        break;
                    }
                }
            }
            if (is_new_corner) hough_edges.push_back(hough_edge);
        }
    }
    if (hough_edges.size() > 4) { // filter out the four strongest edges
        sort(hough_edges.begin(), hough_edges.end(), cmp_edges);
        while (hough_edges.size() > 4) hough_edges.pop_back();
    }
    else if (hough_edges.size() < 4) {
        std::cout << "ERROR: Please set parameter Q larger in file \
            'hough_transform.h' to filter out four edges!" << std::endl;
    }
}

Find Lines

Transform points in hough space to lines in parameter space.

$$m=-\frac {\cos \theta}{\sin \theta}$$
$$b=-\frac {rho}{\sin \theta}$$

Notice the case of line perpendicular to x axis:

$$x=rho$$

/* Transform the points in hough space to lines in parameter space */
void Hough::getLines() {
    for (int i = 0; i < hough_edges.size(); ++i) {
        if (hough_edges[i].angle == 0) { // perpendicular to x axis
            lines.push_back(Line(0, 0, hough_edges[i].rho));
            continue;
        }
        double theta = 1.0 * hough_edges[i].angle * cimg::PI / 180.0;
        double m = -cos(theta) / sin(theta);
        double b = 1.0 * hough_edges[i].rho / sin(theta);
        lines.push_back(Line(m, b));
    }
}

Find Corners

Since the lines returned do not contain any length information, we have to find the end points of each line by calculating the intersections (the corners too) of two lines. Normally,

$$
\begin{cases}
y=m0x+b0 \\
y=m1x+b1
\end{cases}
$$

=>

$$
\begin{cases}
x=\frac{b1-b0}{m0-m1} \\
y==m0*x+b0=m1*x+b1=(m0*x+b0+m1*x+b1)/2
\end{cases}
$$

Also take vertical lines into consideration in the following code.

The following code is a little redundant which calculates each intersection point twice and have to average two version of y for the identical value. Cleaner and neater code are welcome to share!

/* Get four corners of paper sheet by calculate 
*  the intersections of four lines. */
void Hough::getCorners() {
    int x, y;
    double m0, m1, b0, b1;
    for (int i = 0; i < lines.size(); ++i) { // for each line i
        for (int j = 0; j < lines.size(); ++j) { // intersect with line j
            if (j == i || lines[i].end_point_num >= 2 // at most two end points
                || lines[i].dist_o > 0 && lines[j].dist_o > 0)  // both vertical
                continue;
            m0 = lines[i].m;
            b0 = lines[i].b;
            m1 = lines[j].m;
            b1 = lines[j].b;
            if (lines[i].dist_o > 0) { // line i vertical
                x = lines[i].dist_o;
                y = m1 * x + b1;
            }
            else if (lines[j].dist_o > 0) { // line j vertical
                x = lines[j].dist_o;
                y = m0 * x + b0;
            }
            else { // not vertical
                double _x = (b1 - b0) / (m0 - m1);
                x = int(_x);
                // !! Use higher precision _x but not x to calculate y
                y = (m0 * _x + b0 + m1 * _x + b1) / 2; // ensure align at one point
            }

            /* Sometimes the intersects of lines are out of image bound
            *  due to part of paper sheet image or not well aligned lines.
            *  Setting them to the border of image can solve this
            *  problem to some extent. */
            if (x >= 0 - D && x < w + D && y >= 0 - D && y < h + D) {
                if (x < 0) x = 0; else if (x >= w) x = w - 1;
                if (y < 0) y = 0; else if (y >= h) y = h - 1;
                if (lines[i].end_point_num == 0) { // first end point
                    lines[i].x0 = x;
                    lines[i].y0 = y;
                }
                else if (lines[i].end_point_num == 1) { // second end point
                    lines[i].x1 = x;
                    lines[i].y1 = y;
                }
                corners.push_back(Point(x, y));
                ++lines[i].end_point_num;
            }
        }
    }
}

Display Corners and Lines

Lastly, draw and print corners and lines in original rgb image.

/* draw and print corners and lines in original image */
void Hough::displayCornersAndLines() {
    for (int i = 0; i < lines.size(); ++i) {
        // draw
        const unsigned char color_red[] = { 255,0,0 };
        const unsigned char color_yellow[] = { 255,255,0 };
        rgb_img.draw_line(lines[i].x0, lines[i].y0,
            lines[i].x1, lines[i].y1, color_red);
        rgb_img.draw_circle(lines[i].x0, lines[i].y0, 5, color_yellow);
        rgb_img.draw_circle(lines[i].x1, lines[i].y1, 5, color_yellow);

        // print
        if (lines[i].dist_o > 0) {
            std::cout << "Line " << i << ": x = " << lines[i].dist_o << std::endl;
        }
        else {
            char op = lines[i].b > 0 ? '+' : '-';
            std::cout << "Line " << i << ": y = " << lines[i].m
                << "x " << op << abs(lines[i].b) << std::endl;
        }
        std::cout << "Two end points of line "<< i << ": (" << lines[i].x0 <<
            ", " << lines[i].y0 << "), (" << lines[i].x1 <<
            ", " << lines[i].y1 << ")" << std::endl;
    }
}

A Typical Example

From left to right, images of first row are the rgb_img, gray_img.blur(BLUR_SIGMA) and gradients; images of second row are hough_space after houghTransform(), hough_space after getHoughEdges() and rgb_img with detected lines and corners respectively.

• We can see that process of blurring weaks the handwriting and edge of table a lot.
• Contour of paper sheet is extracted after getGradient().
• Performing houghTransform(), we get a beautiful Hough space graph which is stored in matrix hough_space. Its cell value represents the number of curves through any point. Higher cell values are rendered brighter. The four distinctly bright spots are the Hough parameters of the four lines.
• In getHoughEdges() function, we extract them by applying threshold.
• From these spots’ positions, angle and distance from image center(rho) of the four lines in the input image can be determined. Then four lines of the form $y=mx+b$ and their intersections can be determined. Here’s the output indicating line equations and corner coordinates.

Line 0: x = 83
Two end points of line 0: (83, 100), (83, 464)
Line 1: y = 0.0699268x +94.2295
Two end points of line 1: (83, 100), (331, 118)
Line 2: y = -28.6363x +9598.99
Two end points of line 2: (331, 118), (319, 455)
Line 3: y = -0.0699268x +470.145
Two end points of line 3: (83, 464), (319, 455)

Image Warping and Perspective Transform of 2D Image

Theory

Reference

Paper(in chinese): Perspective Image Rectification Based on Improved Hough Transformation and Perspective Transformation
Image Warping Slides by Thomas Funkhouser.
CVPR Slides by Kun Zeng, SYSU.

Futher reading: 2D Image Morphing Algorithms

Concepts

Image filtering: change range of image.
Image warping: change domain of image. Manipulating pixel positions.
Source Image: Image to be used as the reference. The geometry of this image is no changed.
Target Image: this image is obtained by transforming the reference image.
(x,y): coordinates of points in the reference image
(u,v): coordinates of points in the target image
f,g or F,G: x and y component of a transformation function
Control points: Unique points in the reference and target images. The coordinates of corresponding control points in images are used to determine a transformation function.
A Transformation Function: used to compute the corresponding points
Perspective/Projective Transform: Allow a square to be distorted into any quadrilateral. Inverse is also projective. Good when controlling a warp with quadrilaterals, since 4 points in 2D determine the 8 degrees of freedom.

Perspective Transform Parameters Calculation

After obtaining four edges and corners of paper sheet, the next step is mapping. A transformation describes the destination (u,v) for every location (x,y) in the source in this case (quadrilateral->quadrilateral) is perspective transform.

$$u=\frac{ax+by+c}{mx+ly+1}, v=\frac{dx+ey+f}{mx+ly+1}$$

The above equations can also be rewritten as:

$$\begin{bmatrix}u\\v\\ \end{bmatrix} = \begin{bmatrix}x&y&1&0&0&0&-ux&-uy\\0&0&0&x&y&1&-vx&-vy\\ \end{bmatrix} \begin{bmatrix}a\\b\\c\\d\\e\\f\\m\\l\\ \end{bmatrix}$$

In which $a$, $b$, $x$, $d$, $e$, $f$, $m$, $l$ are parameters of perspective transform. Eight equations are need to find out these eight parameters. Mapping four corners(control points) $(x_1,y_1)$, $(x_2,y_2)$, $(x_3,y_3)$, $(x_4,y_4)$ in source image to $(u_1,v_1)$, $(u_2,v_2)$, $(u_3,v_3)$, $(u_4,v_4)$ in destination image with perspective transform, we get

$$\begin{bmatrix}
u_1\\v_1\\u_2\\v_2\\u_3\\v_3\\u_4\\v_4\\ \end{bmatrix} =
\begin{bmatrix}x_1&y_1&1&0&0&0&-u_1x_1&-u_1y_1\\0&0&0&x_1&y_1&1&-v_1x_1&-v_1y_1\\x_2&y_2&1&0&0&0&-u_2x_2&-u_2y_2\\0&0&0&x_2&y_2&2&-v_2x_2&-v_2y_2\\x_3&y_3&3&0&0&0&-u_3x_3&-u_3y_3\\0&0&0&x_3&y_3&1&-v_3x_3&-v_3y_3\\x_4&y_4&4&0&0&0&-u_4x_4&-u_4y_4\\0&0&0&x_4&y_4&1&-v_4x_4&-v_4y_4\\ \end{bmatrix}
\begin{bmatrix}a\\b\\c\\d\\e\\f\\m\\l\\
\end{bmatrix}$$

Or

$$UV=A\times M$$

Eight parameter in matrix form can be calculated by

$$M=A^{-1}\times UV$$

Reverse Mapping

Forward Mapping(Bad): Iterate over source image, sending pixels to destination. With this method, many source pixels can map to same destination pixel and some destination pixels may not be covered.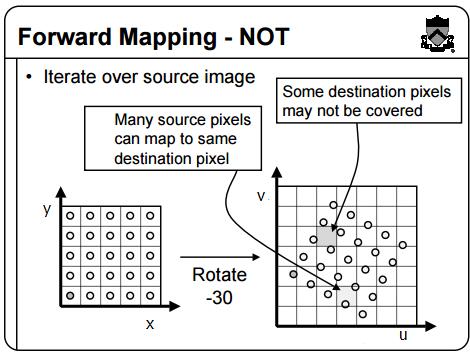

Inverse Mapping(Better): Iterate over destination image, finding pixels from source. (x,y) does not usually have integer coordinates. Must resample source. May oversample, but much simpler! Pseudo-code:

for v = v_min to v_max
    for u = u_min to u_max
        x = F(u, v); y = G(u, v)
        copy pixel at source Src(x, y) to Dest(u, v)

Here the F, G is the inverse transform of $u=\frac{ax+by+c}{mx+ly+1}, v=\frac{dx+ey+f}{mx+ly+1}$. Solve it and get

$$\begin{cases}
x=F(u,v)=\frac{(c-u)(vl-e)-(f-v)(ul-b)}{(um-a)(vl-e)-(vm-d)(ul-b)} \\[2ex]
y=G(u,v)=\frac{(c-u)(vm-d)-(f-v)(um-a)}{(ul-b)(vm-d)-(vl-e)(um-a)} \\[2ex]
\end{cases}$$

Point Sampling with Bilinear Filter: weighted sum of four neighboring pixels.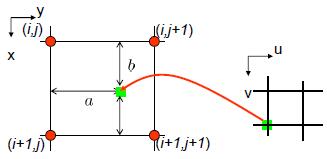

$$Img_{dest}(x,y)=(1-a)(1-b)Img_{src}(i,j) + a(1-b)Img_{src}(i+1,j) + (1-a)b Img_{src}(i,j+1) + (1-a)(1-b)Img_{src}(i+1,j+1)$$

Implementation

Note: the codes has been updated (improved) in GitHub.

Environment

C++ language.

Matrix operations implemented with Eigen (a C++ template library for linear algebra: matrices, vectors, numerical solvers, and related algorithms).
Using Eigen with Microsoft Visual Studio: download (e.g. Eigen 3.3.3), unpack in EIGENDIR (e.g. F:\eigen3.3.3), add EIGENDIR in VS Project(Project->Properties->C/C++->General->Additional Include Directories->F:\eigen3.3.3;), include header file (e.g. #include<Eigen/Dense>), use(e.g. Eigen::MatrixXf UV(8, 1);).

Image processing operations implemented with The CImg Library.
Usage: download CImg.h file, include by include "CImg.h"

Codes

• Step1: Before mapping, we need to get four control points in source image and destination image respectively. Destination corners can be easily defined

const float W = 410, H = 594;
const float u1 = 0, v1 = 0, // top-left
        u2 = W - 1, v2 = 0, // top-right
        u3 = 0, v3 = H - 1, // bottom-left
        u4 = W - 1, v4 = H - 1; // bottom-right

Source corners need to be in the same order as destination corners so as to map one by one correctly. The following method is a bit tricky and may not apply to all situations but for most of cases it works well.

/* Compare function for corners sort.The corner
closest to original point rank first. */
bool cmp_corners(Point c1, Point c2) {
    return (c1.x * c1.x + c1.y * c1.y)
        < (c2.x * c2.x + c2.y * c2.y);
}

std::vector<Point> Hough::getOrderedCorners() {
    // Usually, if paper sheet is placed vertically(do not need strictly)
    // corners are ordered in top-left, top-right, bottom-left, bottom-right
    //  position by sorting (compare by the distance from original point)
    sort(corners.begin(), corners.end(), cmp_corners);
    for (int i = 0; i < corners.size(); i += 2)
        ordered_corners.push_back(Point(corners[i].x, corners[i].y));
    
    // fine tuning the corners to white paper sheet if not
    // aims to crop black background
    const int SHIFT = 3;
    if (rgb_img(ordered_corners[0].x, ordered_corners[0].y) < 125) {
        ordered_corners[0].x += SHIFT;
        ordered_corners[0].y += SHIFT;
    }
    if (rgb_img(ordered_corners[1].x, ordered_corners[1].y) < 125) {
        ordered_corners[1].x -= SHIFT;
        ordered_corners[1].y += SHIFT;
    }
    if (rgb_img(ordered_corners[2].x, ordered_corners[2].y) < 125) {
        ordered_corners[2].x += SHIFT;
        ordered_corners[2].y -= SHIFT;
    }
    if (rgb_img(ordered_corners[3].x, ordered_corners[3].y) < 125) {
        ordered_corners[3].x -= SHIFT;
        ordered_corners[3].y -= SHIFT;
    }
    
    // If horizontally, top-left and bottom-left corners,
    // top-right and bottom-tight corners need swapping.
    // If not, it seems like look from the back of the paper
    // I roughly judge it by image's width and height
    // but not paper sheet's for convenience.
    if (w > h) { 
        int tmpx = ordered_corners[1].x;
        int tmpy = ordered_corners[1].y;
        ordered_corners[1].x = ordered_corners[0].x;
        ordered_corners[1].y = ordered_corners[0].y;
        ordered_corners[0].x = tmpx;
        ordered_corners[0].y = tmpy;
        tmpx = ordered_corners[3].x;
        tmpy = ordered_corners[3].y;
        ordered_corners[3].x = ordered_corners[2].x;
        ordered_corners[3].y = ordered_corners[2].y;
        ordered_corners[2].x = tmpx;
        ordered_corners[2].y = tmpy;
    }
    return ordered_corners;
}

• Step2: calculate perspective transform parameters

void Warping::perspectiveTransform() {
    Eigen::MatrixXf UV(8, 1);
    Eigen::MatrixXf M = Eigen::MatrixXf::Constant(8, 1, 0);
    Eigen::MatrixXf A(8, 8);
    UV << u1, v1, u2, v2, u3, v3, u4, v4;
    A << x1, y1, 1, 0,  0,  0, -u1*x1, -u1*y1,
         0,  0,  0, x1, y1, 1, -v1*x1, -v1*y1,
         x2, y2, 1, 0,  0,  0, -u2*x2, -u2*y2,
         0,  0,  0, x2, y2, 1, -v2*x2, -v2*y2,
         x3, y3, 1, 0,  0,  0, -u3*x3, -u3*y3,
         0,  0,  0, x3, y3, 1, -v3*x3, -v3*y3,
         x4, y4, 1, 0,  0,  0, -u4*x4, -u4*y4,
         0,  0,  0, x4, y4, 1, -v4*x4, -v4*y4;
    M = A.inverse() * UV;
    a = M(0,0), b = M(1, 0), c = M(2, 0), d = M(3, 0),
        e = M(4, 0), f = M(5, 0), m = M(6, 0), l = M(7, 0);
}

• Step3: reverse mapping

void Warping::reverseMapping() {
    cimg_forXYC(dest_A4, u, v, c) { // c indicates color channels
        float x = getXTransformInv(u, v);
        float y = getYTransformInv(u, v);
        dest_A4(u, v, c) = bilinearInterpolate(x, y, c);
    }
}

• Auxiliary function

float Warping::getXTransformInv(int u, int v) {
    return ((c - u)*(v*l - e) - (f - v)*(u*l - b)) /
        ((u*m - a)*(v*l - e) - (v*m - d)*(u*l - b));
}

float Warping::getYTransformInv(int u, int v) {
    return ((c - u)*(v*m - d) - (f - v)*(u*m - a)) /
        ((u*l - b)*(v*m - d) - (v*l - e)*(u*m - a));
}

float Warping::bilinearInterpolate(float x, float y, int c) {
    int i = floorf(x), j = floorf(y);
    float a = x - i, b = y - j;
    return (1 - a)*(1 - b)*src(i, j, c) + a*(1 - b)*src(i + 1, j, c)
        + (1 - a)*b*src(i, j + 1, c) + a*b*src(i + 1, j + 1, c);
}

Results

All source images have resized to around 400px*539px, 631KB to save space and process time.
Following are original image, image with mark of edges and corners and cropped image respectively each row.

Pros and Cons

Pros: Most of the lines and corners are detected correctly in different circumstances(background, angle, noise, handwriting, light, shadow, imcomple paper sheet etc.) without tuning parameters for each image seperately.
Cons: Cropped results is blureed due to bilinear interpolation. A few of the lines and corners are not aligned perfectly. There are several reasons:

• “Due to imperfection errors in the edge detection step, there will usually be errors in the accumulator space, which may make it non-trivial to find the appropriate peaks, and thus the appropriate lines.”
• High-precision type like double is used for parameters like m and b while some parameters like angle, rho and cordinates of points have to use type like int for pixel by pixel calculation and storage in matrix. Error is produced when casting type.
• The edges in images are not straight.