Produce a “morph” animation of one image into another image, which involves two parts: cross dissolving and affine warping.

Approaches

GOAL

Morph a blue triangle tri1 to a pink triangle tri2 according to their three vertices respectively.

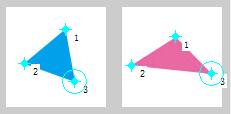
Left: tri1; Middle: corresponding vertices of tri1 and tri2; Right: tri2

The ideal transition is as follow.

Left: tri1 morph to tri2; Middle: tri1 morph to tri2 slowly in 5 frames; Right: each frame of slow transition

Process

Firstly, slice two images into triangles in the same way. Four corners of images are appended so as to cover entire image with triangles.

Then, warp tri1 from shape of tri1 to shape of tri2 for each triangle respectively. Do the same for tri2 (warp tri2 from shape of tri1 to shape of tri2).
Lastly, perform cross-dissolve of two warp’s colors.

Left: warp of tri1; Middle: warp of tri2; Right: cross-dissolve of two warp’s color

Details

Morphing is defined as the animated transformation of one image into another. We do it by producing sequence of frames. As shown above, morphing involves two parts: cross dissolving and warping.

Cross dissolving is linear interpolation to fade from one image to another. In another word, interpolate a value from 0 to 1 and use $A*value + B*(1-value)$ as the frame value.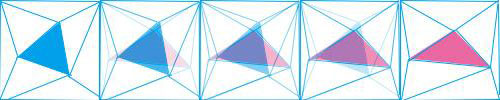

Simply using cross-dissolving will cause double-exposure effect in misaligned regions. So we need to align the two images before cross dissolving

Warping is used for this purpose. Pixels are “moving” from frame to frame in this process. A mapping rule is used to determine the way in which the pixels in one image should be mapped to the pixels in the other image.
Here I use affine transformation for warping triangles. Given two triangles ABC and A’B’C’ in 2D, the transformation matrix to transfer all pixels from one to the other is

$$
\begin{bmatrix}x’ \cr y’ \cr 1 \cr \end{bmatrix} =
\begin{bmatrix}a & b & c \cr d & e & f \cr 0 & 0 & 1 \cr \end{bmatrix}
\begin{bmatrix}x \cr y \cr 1 \cr \end{bmatrix}
$$

a,b,c,d,e,f are constants and x’, y’, x, y are 1-by-3 vectors. (e.g. $x=[x_A,x_B,x_C]$).
Write the formula in short: $p’=Ap$.
In this way, two images are sliced into triangles one-to-one. The one-to-one relationship between pair of triangle in two images is fixed for smoothly transformation. That is to say, triangle#n of frame t is always mapped to triangle#n of frame t+1.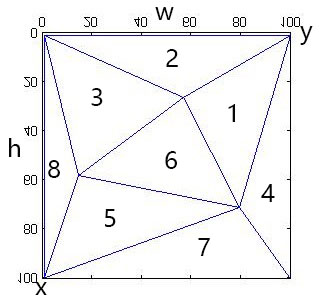

Each pair of triangle has a transformation matrix for mapping. This matrix will change from frame to frame since the shape and position of triangles will change from frame to frame.
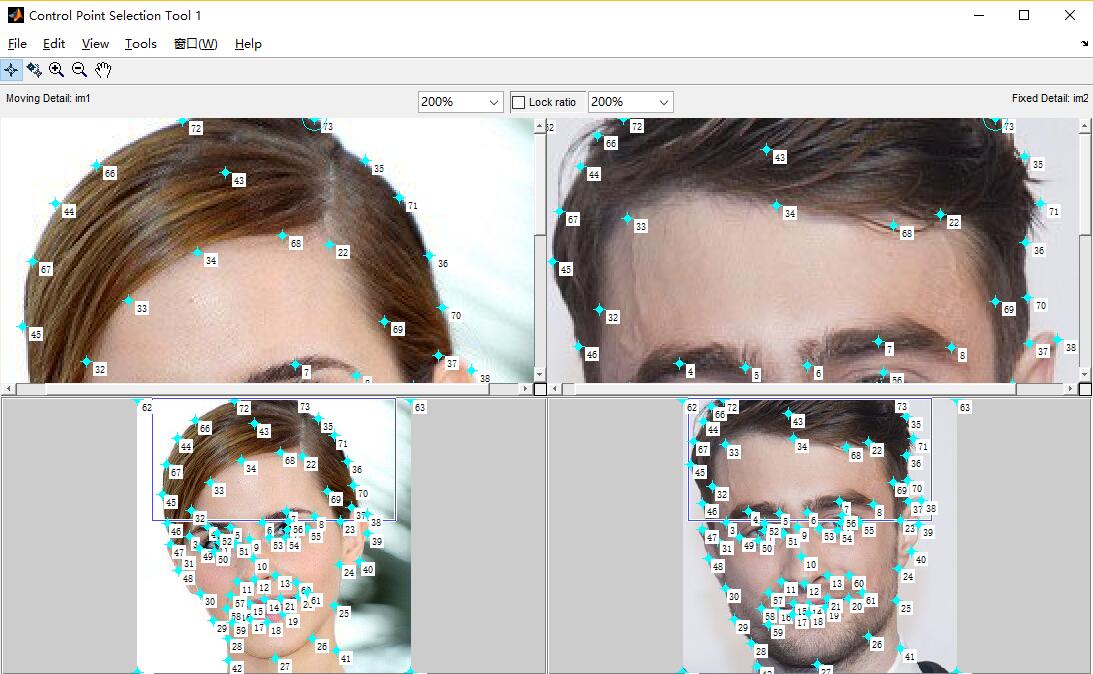
Now the problem is how to compute $A$. Since $p$ is a $3\times 3$ square matrix, it is invertible. $A=p’p^{-1}$. Points $p’$ and $p$ are specified by six vertices in each pair of triangles. We call them control pixels/points, which usually specify prominant features in the images. Select points on features that we want to align during the morph in a consistent manner using the same ordering of all keypoints (the more points, the better the morph, generally): eyes, ears, nose, mouth, etc.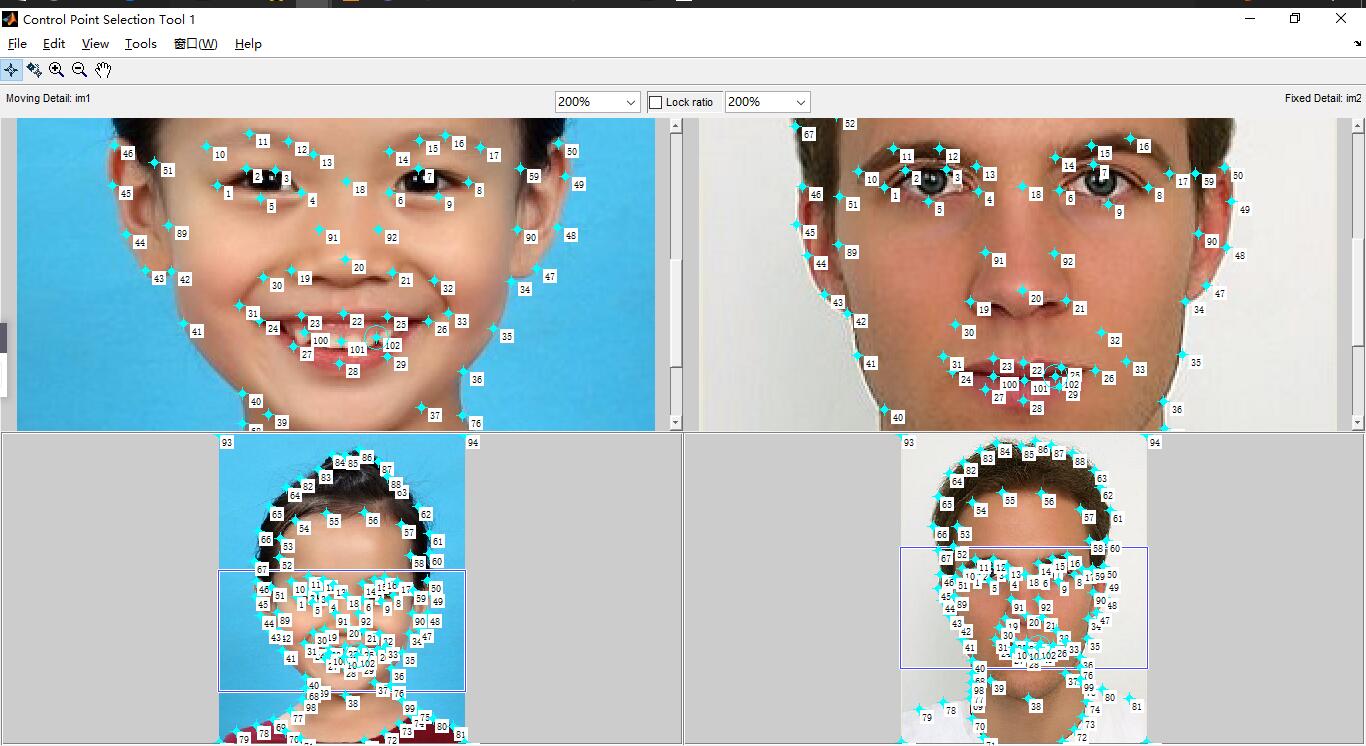

Having known $A$, the coordinate transform matrix, the non-marked points $p’$ (all pixels in triangles except vertices) can be computed from source points $p$. There are two ways to do this.

Forward warping: send each pixel $p$ to its corresponding location $p’=Ap$ in the second image.
Inverse warping: get each pixel $p’$ from its corresponding location $p=A^{-1}p’$ in the first image.

Inverse warping is a better way. See my discussion in A4 paper sheet detection and cropping for more details.

Implementation

Language: Matlab.

Attention: Hopefully my comments are detailed enough, I will not talk a lot in this part. The code below is an excerpt; full source is here.

The process is clear. Firstly, define correspondences and then produce each frame of the morph sequence specified by a fraction from 0 to 1.

[im1_pts, im2_pts, tri] = ...
    define_correspondences(im1, im2, im1_pts_path, im2_pts_path);
for frac = linspace(0, 1, frames_num)
    morphed_im = morph(im1, im2, im1_pts, im2_pts, tri, frac, frac);
end

Defining Correspondences

function [im1_pts, im2_pts, tri] = define_correspondences(...
    im1, im2, im1_pts_path, im2_pts_path)
%DEFINE_CORRESPONDENCES Define pairs of corresponding points.
%   returns pairs of corresponding points on the two images specify by 
%   their paths and the triangulation structure tri at midway shape.
[im1_pts, im2_pts] = cpselect(im1, im2, 'Wait', true);
pts_mean = (im1_pts + im2_pts) / 2;
tri = delaunay(pts_mean);
end

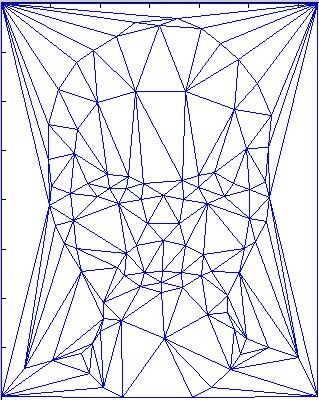
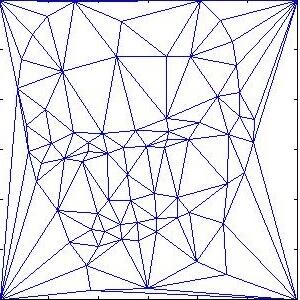
As I have mentioned, the one-to-one relationship between pair of triangle in two images is fixed. The triangulation is computed by the mean of the two point sets to lessen the potential triangle deformations. Each row of tri specifies a triangle defined by indices with respect to the points. In other word, tri is a matrix storing three vertices’s indexes of each triangle. The relative order of triangles will not change so we can tell which triangle from source image corresponds to which triangle in destination image.

The Morph Sequence

function morphed_im = morph(...
    im1, im2, im1_pts, im2_pts, tri, warp_frac, dissolve_frac)
%MORPH Morph image.
%   [MORPHED_IM]=MORPH(IM1,IM2,IM1_PTS,IM2_PTS,TRI,WARP_FRAC,DISSOLVE_FRAC) 
%   returns a warp between im1 and im2 using point correspondences defined 
%   in im1_pts and im2_pts (which are both n-by-2 matrices of (x,y) 
%   locations) and the triangulation structure tri. 
%   The parameters warp_frac and dissolve_frac control shape warping and 
%   cross-dissolve, respectively. For interpolation, both parameters lie
%   in the range [0,1]. They are the only parameters that will vary from
%   frame to frame in the animation.
% Images im1 and im2 are first warped into an intermediate shape
% configuration controlled by warp_frac.
inter_shape_pts = warp_frac * im2_pts + (1 - warp_frac) * im1_pts;
im1_warp = affine_warp(im1, im1_pts, inter_shape_pts, tri);
im2_warp = affine_warp(im2, im2_pts, inter_shape_pts, tri);
% And then cross-dissolved according to dissolve_frac.
morphed_im = dissolve_frac * im2_warp + (1 - dissolve_frac) * im1_warp;
end

Affine warp

This part is a little tricky in implementation.

function warp_im = affine_warp(im, from_pts, to_pts, tri)
%AFFINE_WARP Affine warp.
%   [WARP_IM] = AFFINE_WARP(IM,FROM_PTS,TO_PTS,TRI) 
%   returns an affine warp for each triangle in the triangulation from the
%   original image into a new shape using point correspondences defined 
%   in from_pts and to_pts (which are both n-by-2 matrices of (x,y) 
%   locations) and the triangulation structure tri.
warp_im = im;
[h, w, channel] = size(im);
[Y, X] = meshgrid(1:h, 1:w);
%t(i) gives the index(into tri)of the first triangle containing (X(i),Y(i))
t = mytsearch(to_pts(:, 1), to_pts(:, 2), tri, X, Y); %search triangulation
tri_index_map = zeros(size(t));
valid_tri_idx = ~isnan(t); % t(i) is NaN for points not in any triangle
tri_index_map(valid_tri_idx) = t(valid_tri_idx);
% inverse warp of all pixels
for i = 1:size(tri,1) % for each triangle
    [col, row] = find(tri_index_map == i); % find out all points in it
    p2 = transpose([col, row, ones(size(col,1),1)]); % [x';y';1]
    % computing an affine transformation matrix A between two triangles
    A = computeAffine(from_pts(tri(i,:),:), to_pts(tri(i,:),:));
    p = pinv(A) * p2; % p2=Ap -> p=A^(-1)p2
    p = floor(p); % index should be integer
    
    % avoid out of bound
    % omit......
    % warp_im(p2(1,:),p2(2,:),:)=im(p(1,:),p(2,:),:); % large memory&time!
    p_ind = sub2ind([h, w], p(2,:), p(1,:)); % convert to linear indices
    p2_ind = sub2ind([h, w], p2(2,:), p2(1,:));
    
    warp_im(p2_ind) = im(p_ind); % first channel
    if channel == 3
        warp_im(p2_ind + w*h) = im(p_ind + w*h); % second channel
        warp_im(p2_ind + 2*w*h) = im(p_ind + 2*w*h); % third channel
    end
end
end

Results and Analysis

Image morphing can be applied to any object, but obviously it will have better effect for objects with similar structure and uniform background. Human faces set an example.

Human faces

Girl Morph to Boy

For human faces, about 60 control points are enough. Here I use about 100 control points for fine-grained result. From the girl to the boy, there are 11 frames of animation between them where each frame is displayed for 0.1 second.

Here are the “mid-way” faces of frame 2, 4, 6, 8, 10. The fourth image is the triangulation of average face(frame 6)

Watson Morph to Daniel

Can you tell whom this average face are combined of???

Emma Watson and Daniel Radcliffe!

The selection of control points for hair is tricky since one is round while the other is square. Anyway, just select a set of points you want to map.

Average Face of Chinese Beauty

Game time! Take a guess.

As you can seen, these “combined” beauties still have rather real and clear faces which perfectly combine their two “source” beauties’s features. But the backgrounds and headwears have double-exposure effect due to lacking corresponding aligned objects.

Peking Opera Mask Morphing

In fact, my original intention was to produce a morphing music video of the traditional Chinese Peking Opera masks! At first glance, its rather simple because all masks are oval, symmetrical, with mouth/eyes/nose/ears and without background. However, I gave up after morphing a pair of masks.

I used more than 100 control points and felt rather difficult to find corresponding control points. And this is the simplest one! Take a look at the following masks.